Calculus with Vector-Valued Functions

Limits and derivatives and integrals of vector valued functions are defined component wise:

\(\displaystyle \lim\limits_{t \to 0} \bm{r}(t) \!=\! \Bigl\langle \lim_{t \to 0} x(t), \lim_{t \to 0} y(t), \lim_{t \to 0} z(t) \Bigr\rangle \)

\(\displaystyle \bm{r}'(t) \!=\! \frac{\mathrm{d}\bm{r}}{\mathrm{d}{t}} \!=\! \lim\limits_{h \to 0} \frac{\bm{r}(t+h)-\bm{r}(t)}{h} \!=\! \bigl\langle x'(t), y'(t), z'(t) \bigr\rangle \)

\( \int \!\bm{r}(t) \mathrm{d}t \!=\! \Bigl\langle \int \!x(t) \mathrm{d}t, \int \!y(t) \mathrm{d}t, \int \!z(t) \mathrm{d}t \Bigr\rangle \)

A vector-valued function \(\bm{r}\) is continuous at \(t = a\) if \(\lim_{t \to a} \bm{r}(t) = \bm{r}(a).\) A vector-valued function is smooth if the derivatives of its component functions exist for all orders. A curve itself is smooth if it has a smooth parameterization. A parameterization \(\bm{r}(t)\) of a curve is regular if \(\bm{r}'(t) \neq \bm{0}\) for any \(t\) — the parameterization never stops along the curve. Analogously, a parameterization \(\bm{r}(s,t)\) of a surface is regular if \(\frac{\mathrm{d}\bm{r}}{\mathrm{d}s}\) and \(\frac{\mathrm{d}\bm{r}}{\mathrm{d}t}\) are not parallel (not linearly dependent) at any point.

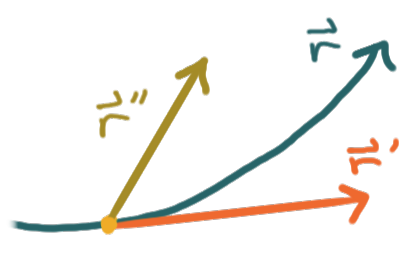For a curve \(C\) with parameterization \(\bm{r}\) that represents the position of a particle along that curve in space, the derivative \(\bm{r}'(t)\) represents the velocity vector \(\bm{v}(t)\) of the particle, and likewise \(\bm{r}''(t)\) represents its acceleration vector \(\bm{\alpha}(t).\) The line with parameterization \(\bm{r}(t_0) + \bm{r}'(t_0)t\) will be tangent to the curve \(C\) at the point \(\bm{r}(t_0).\)

For a projectile fired from the origin within the \(xy\)-plane at an angle of inclination \(\theta\) and initial velocity \(v_0\) under in the influence of gravitational acceleration \(g\) in the negative \(y\) direction, the parametric equations that describe its trajectory are:

\(\displaystyle x(t) = \big(v_0 \cos(\theta)\big)t\)

\(\displaystyle y(t) = \big(v_0 \sin(\theta)\big)t - \frac{1}{2}gt^2\)