For a rectangular expanse \(E = [a,b] \times [c,d] \times [r,s]\) in \(\mathbf{R}^3\) and a function \(f\colon E \to \mathbf{R},\) the triple integral \(\iiint_E f \,\mathrm{d}V\) is equal to an iterated integral that can be evaluated “one variable at a time” by applying the fundamental theorem of calculus thrice. Per Fubini’s Theorem, if \(f\) is continuous on the expanse then the order of the differentials \(\mathrm{d}x\) and \(\mathrm{d}y\) and \(\mathrm{d}z,\) along with their bounds, may be freely permuted. \[ \iiint\limits_E f \,\mathrm{d}V \;\;=\;\; \int\limits_a^b\left(\int\limits_c^d\left(\int\limits_r^s f(x,y,z) \,\mathrm{d}z\right)\mathrm{d}y\right)\mathrm{d}x \;\;=\;\; \int\limits_a^b\int\limits_c^d\int\limits_r^s f(x,y,z) \,\mathrm{d}z\,\mathrm{d}y\,\mathrm{d}x \]
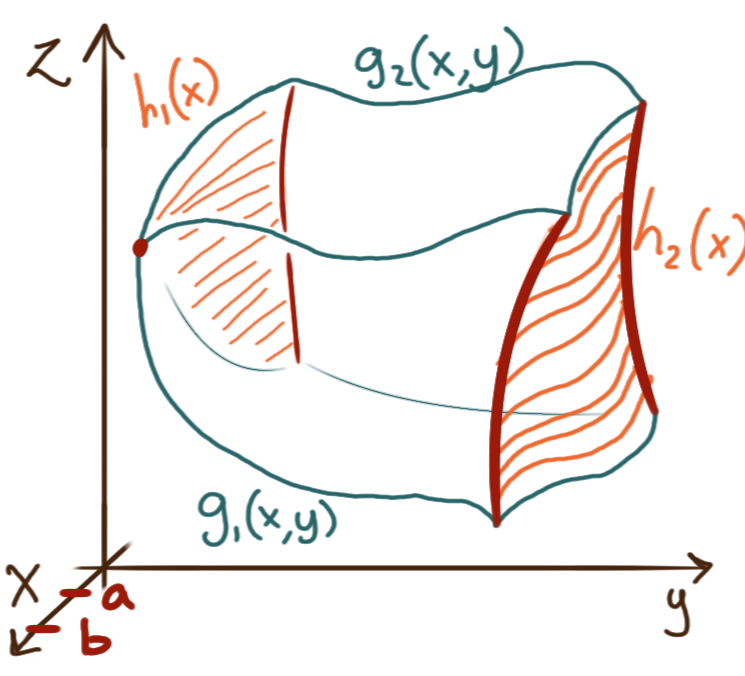If \(E\) is not rectangular but has a boundary
that can be described analytically as the graphs of functions
then the triple integral \(\iiint_E f \,\mathrm{d}V\) can still be computed.
For example, if for each \(x\) between \(a\) and \(b\)
the area of the corresponding cross section parallel to the \(yz\)-plane
can be computed as a double integral with,
for each \(x,\) the variable \(y\) sweeping from \(h_1(x)\) to \(h_2(x),\)
and for each \(x\) and \(y,\) the variable \(z\) sweeping from \(g_1(x,y)\) to \(g_2(x,y),\)
then
\[
\iiint\limits_E f \,\mathrm{d}V
\;\;=\;\;
\int\limits_a^b\int\limits_{h_1(x)}^{h_2(x)}\int\limits_{g_1(x,y)}^{g_2(x,y)} f(x,y,z) \,\mathrm{d}z\,\mathrm{d}y\,\mathrm{d}x
\,.
\]
Note, as an iterated integral, the function-bounds
are always expressed in terms of variables that have yet to be integrated.
And per Fubini’s Theorem, the order of integration may be changed
by permuting the differentials \(\mathrm{d}x\) and \(\mathrm{d}y\) and \(\mathrm{d}z,\)
but the functions that describe the bounds would also have to change
to reflect how the expanse is being “swept out.”