Recall that a point in space \(\mathbf{R}^3\) with rectangular (Cartesian) coordinates \((x,y,z)\)
can be expressed in cylindrical coordinates as
\((r, \theta, z) = \bigl(\sqrt{x^2+y^2}, \operatorname{atan2}(y,x), z\bigr).\)
For an expanse \(E\) with boundary that can be described analytically
by the functions \({z = g_1(r,\theta)}\) and \({z = g_2(r,\theta)}\) in the \(z\) direction,
and \({r = h_1(\theta)}\) and \({r = h_2(\theta)}\) in the radial direction
and for azimuth \(\theta\) between \({\theta = \alpha}\) and \({\theta = \beta},\)
the triple integral \(\iiint_E f \,\mathrm{d}V\) of a function \(f \colon E \to \mathbf{R}\)
can be calculated as an iterated integral
with an additional integrating factor of \({\color{maroon} r}.\)
\[
\iiint\limits_E f \,\mathrm{d}V
\;\;=\;\;
\int\limits_{\alpha}^{\beta}
\int\limits_{h_1(\theta)}^{h_2(\theta)}
\int\limits_{g_1(r,\theta)}^{g_2(r,\theta)}
f\bigl(r\cos(\theta),r\sin(\theta),z\bigr) \,{\color{maroon} r} \,\mathrm{d}z\,\mathrm{d}r\,\mathrm{d}\theta
\]
Recall that a point in space \(\mathbf{R}^3\) with rectangular (Cartesian) coordinates \((x,y,z)\)
can be expressed in spherical coordinates as
\((\rho, \theta, \varphi) = \bigl(\sqrt{x^2+y^2+z^2}, \operatorname{atan2}(y,x), \operatorname{arccos}(z/\rho)\bigr).\)
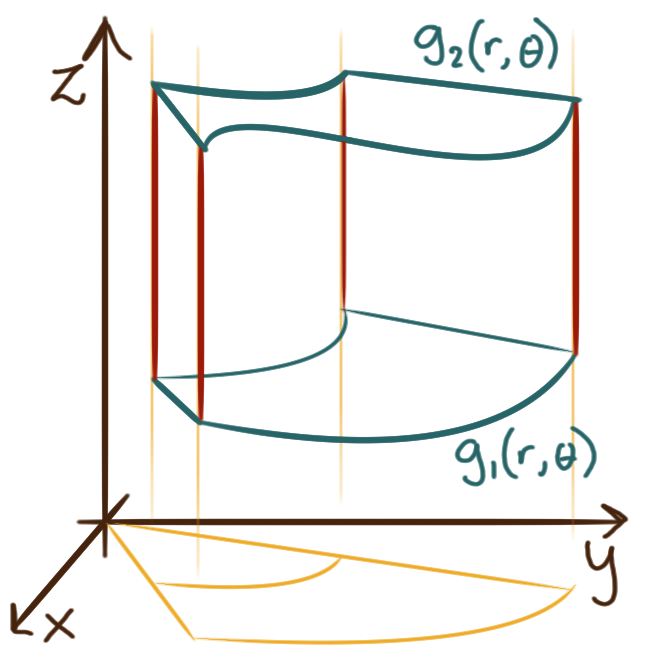
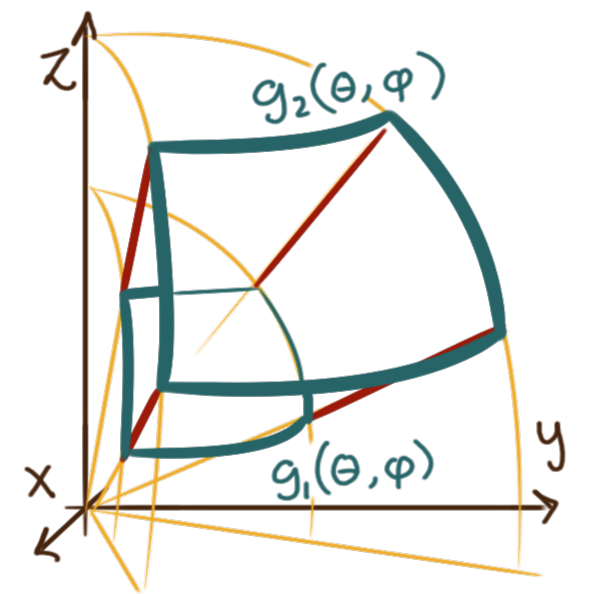For an expanse \(E\) with boundary that can be described analytically
by the functions \({\rho = g_1(\theta, \varphi)}\) and \({\rho = g_2(\theta, \varphi)}\) in the radial direction,
and \({\theta = h_1(\varphi)}\) and \({\theta = h_2(\varphi)}\) in the azimuthal direction
and for zenith \(\varphi\) between \({\varphi = \alpha}\) and \({\varphi = \beta},\)
the triple integral \(\iiint_E f \,\mathrm{d}V\) of a function \(f \colon E \to \mathbf{R}\)
can be calculated as an iterated integral
with an additional integrating factor of \({\color{maroon} \rho^2\sin(\varphi)}.\)
\[
\iiint\limits_E f \,\mathrm{d}V
\;\;=\;\;
\int\limits_{\alpha}^{\beta}
\int\limits_{h_1(\varphi)}^{h_2(\varphi)}
\int\limits_{g_1(\theta, \varphi)}^{g_2(\theta, \varphi)}
f\bigl(\rho\sin(\varphi)\cos(\theta), \rho\sin(\varphi)\sin(\theta), \rho\cos(\varphi)\bigr)
\,{\color{maroon} \rho^2\sin(\varphi)} \,\mathrm{d}\rho\,\mathrm{d}\theta\,\mathrm{d}\varphi
\]