In three-dimensional space, we add a \(z\)-axis perpendicular (orthogonal) to the usual \(x\)- and \(y\)-axis to create a rectangular (Cartesian) coordinate system called \(xyz\)-space. The \(z\)-axis is oriented relative to the \(xy\)-plane in accordance to the right-hand rule. Any pair of axes span a coordinate plane, and these coordinate planes split \(xyz\)-space into eight octants. Each point can be described by a ordered triple \((x,y,z).\) Given two points \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2),\) the distance between them is \( \sqrt{(x_2\!-\!x_1)^2+(y_2\!-\!y_1)^2+(z_2\!-\!z_1)^2}. \)
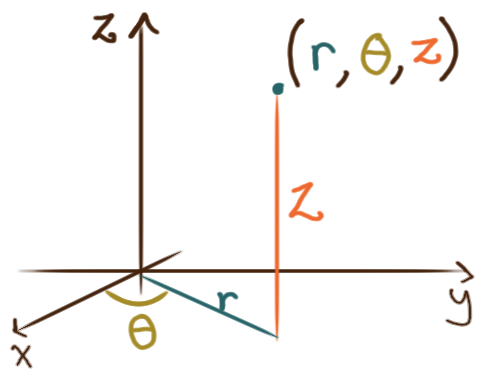 In cylindrical coordinates,
a point is referred to by a triple \((r, \theta, z)\)
where \(r\) and \(\theta\) are
the polar coordinates of the point in the \(xy\)-plane
and \(z\) is the height of the point above the \(xy\)-plane.
To convert between rectangular and cylindrical coordinates:
\[ \begin{align*}
(x,y,z) &\longrightarrow \Big(\sqrt{x^2+y^2}, \operatorname{atan2}(y,x), z\Big)
\\ \big(r\cos(\theta), r\sin(\theta),z\big) &\longleftarrow (r,\theta,z)
\end{align*} \]
In cylindrical coordinates,
a point is referred to by a triple \((r, \theta, z)\)
where \(r\) and \(\theta\) are
the polar coordinates of the point in the \(xy\)-plane
and \(z\) is the height of the point above the \(xy\)-plane.
To convert between rectangular and cylindrical coordinates:
\[ \begin{align*}
(x,y,z) &\longrightarrow \Big(\sqrt{x^2+y^2}, \operatorname{atan2}(y,x), z\Big)
\\ \big(r\cos(\theta), r\sin(\theta),z\big) &\longleftarrow (r,\theta,z)
\end{align*} \]
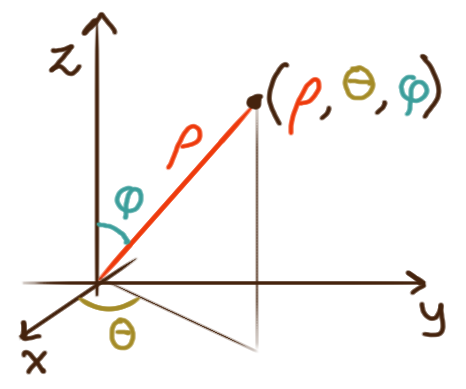 In spherical coordinates,
a point is referred to by a triple \((\rho, \theta, \varphi)\)
where \(\rho\) is the point’s distance from the origin,
\(\theta\) (the azimuth) is the angle in the \(xy\)-plane above which it lies,
and \(\varphi\) (the zenith) is the angle at which it’s declined from the positive \(z\)-axis.
To convert between rectangular and spherical coordinates:
\[
\begin{align*}
(x,y,z) &\longrightarrow \Biggl(\sqrt{x^2+y^2+z^2}, \operatorname{atan2}(y,x), \operatorname{arccos}\biggl(\frac{z}{\sqrt{x^2+y^2+z^2}}\biggr)\Biggr)
\\ \Big(\rho\sin(\varphi)\cos(\theta), \rho\sin(\varphi)\sin(\theta), \rho\cos(\varphi)\Big) &\longleftarrow (\rho,\theta,\varphi)
\end{align*}
\]
In spherical coordinates,
a point is referred to by a triple \((\rho, \theta, \varphi)\)
where \(\rho\) is the point’s distance from the origin,
\(\theta\) (the azimuth) is the angle in the \(xy\)-plane above which it lies,
and \(\varphi\) (the zenith) is the angle at which it’s declined from the positive \(z\)-axis.
To convert between rectangular and spherical coordinates:
\[
\begin{align*}
(x,y,z) &\longrightarrow \Biggl(\sqrt{x^2+y^2+z^2}, \operatorname{atan2}(y,x), \operatorname{arccos}\biggl(\frac{z}{\sqrt{x^2+y^2+z^2}}\biggr)\Biggr)
\\ \Big(\rho\sin(\varphi)\cos(\theta), \rho\sin(\varphi)\sin(\theta), \rho\cos(\varphi)\Big) &\longleftarrow (\rho,\theta,\varphi)
\end{align*}
\]