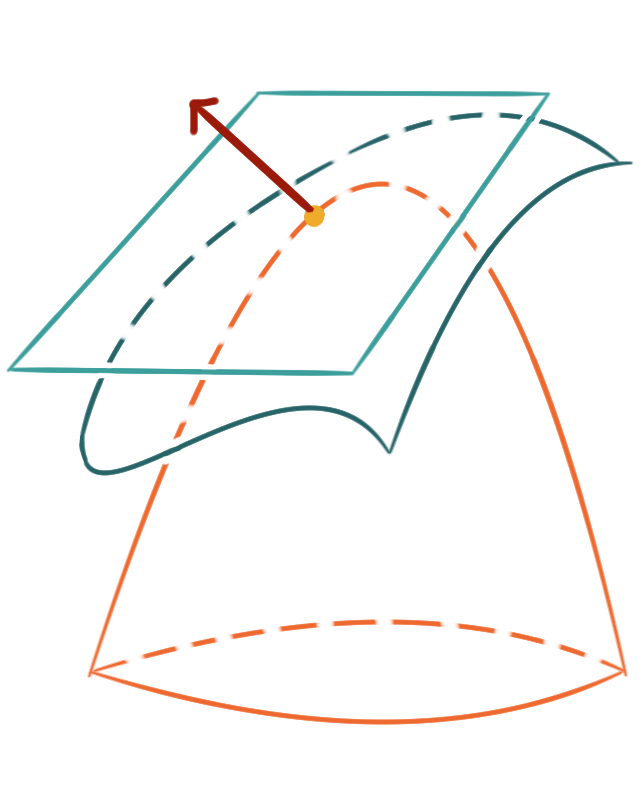
 For a multi-variable function \(f \colon \mathbf{R}^2 \to \mathbf{R}\)
the equation for the plane tangent to the graph \(z = f(x,y)\)
at the point \(\bigl(x_0, y_0, z_0\bigr)\) where \(z_0 = f(x_0, y_0)\) is
\[ z = f(x_0, y_0) + f_x(x_0, y_0)\bigl(x - x_0\bigr) + f_y(x_0, y_0)\bigl(y - y_0\bigr)\,. \]
Writing this equation in the usual template for a plane,
\[ f_x(x_0, y_0)\bigl(x-x_0\bigr) + f_y(x_0, y_0)\bigl(y-y_0\bigr) - \bigl(z-z_0\bigr) = 0\,, \]
implies that the vector
\(\bigl\langle f_x(x_0, y_0), f_y(x_0, y_0), -1 \bigr\rangle\)
will be normal to the plane, and thus the graph, at that point.
Beyond tangent planes (linear approximations),
Taylor’s Theorem holds for multivariable functions,
giving us a series representation of any smooth function
\(f\colon \mathbf{R}^2\to\mathbf{R},\)
per some “anchor” point \((x_0,y_0,z_0)\) on the function’s graph:
\[ f(x,y) = \sum_{n=0}^{\infty}\sum_{k=0}^{n}\frac{f_{x_{k} y_{n-k}}(x_0,y_0)}{k!(n-k)!}\bigl(x-x_0\bigr)^k\bigl(x-y_0\bigr)^{n-k} \]
Explicitly, the second-order Taylor approximation
to \(f\) at \((x_0,y_0)\) gives the paraboloid
\[
z = f(x_0, y_0)
+ f_x(x_0, y_0)\bigl(x - x_0\bigr) + f_y(x_0, y_0)\bigl(y - y_0\bigr)
+ \frac{f_{xx}(x_0, y_0)}{2}\bigl(x - x_0\bigr)^2
+ f_{xy}(x_0, y_0)\bigl(x - x_0\bigr)\bigl(y - y_0\bigr)
+ \frac{f_{yy}(x_0, y_0)}{2}\bigl(y - y_0\bigr)^2
\,.
\]
For a multi-variable function \(f \colon \mathbf{R}^2 \to \mathbf{R}\)
the equation for the plane tangent to the graph \(z = f(x,y)\)
at the point \(\bigl(x_0, y_0, z_0\bigr)\) where \(z_0 = f(x_0, y_0)\) is
\[ z = f(x_0, y_0) + f_x(x_0, y_0)\bigl(x - x_0\bigr) + f_y(x_0, y_0)\bigl(y - y_0\bigr)\,. \]
Writing this equation in the usual template for a plane,
\[ f_x(x_0, y_0)\bigl(x-x_0\bigr) + f_y(x_0, y_0)\bigl(y-y_0\bigr) - \bigl(z-z_0\bigr) = 0\,, \]
implies that the vector
\(\bigl\langle f_x(x_0, y_0), f_y(x_0, y_0), -1 \bigr\rangle\)
will be normal to the plane, and thus the graph, at that point.
Beyond tangent planes (linear approximations),
Taylor’s Theorem holds for multivariable functions,
giving us a series representation of any smooth function
\(f\colon \mathbf{R}^2\to\mathbf{R},\)
per some “anchor” point \((x_0,y_0,z_0)\) on the function’s graph:
\[ f(x,y) = \sum_{n=0}^{\infty}\sum_{k=0}^{n}\frac{f_{x_{k} y_{n-k}}(x_0,y_0)}{k!(n-k)!}\bigl(x-x_0\bigr)^k\bigl(x-y_0\bigr)^{n-k} \]
Explicitly, the second-order Taylor approximation
to \(f\) at \((x_0,y_0)\) gives the paraboloid
\[
z = f(x_0, y_0)
+ f_x(x_0, y_0)\bigl(x - x_0\bigr) + f_y(x_0, y_0)\bigl(y - y_0\bigr)
+ \frac{f_{xx}(x_0, y_0)}{2}\bigl(x - x_0\bigr)^2
+ f_{xy}(x_0, y_0)\bigl(x - x_0\bigr)\bigl(y - y_0\bigr)
+ \frac{f_{yy}(x_0, y_0)}{2}\bigl(y - y_0\bigr)^2
\,.
\]