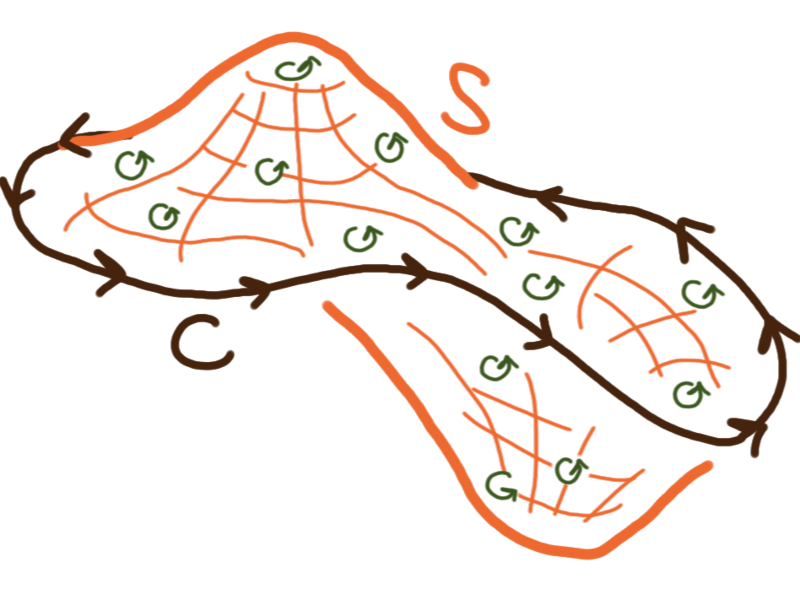
 Stokes’ Theorem
(or the Kelvin-Stokes Theorem,
or the Curl Theorem) —
for an oriented piecewise-smooth surface \(S\) whose boundary \(C = \partial S\)
is a simple, closed, piecewise-smooth, positively-oriented curve,
and a vector field \(\bm{F}\) whose components
have continuous partial derivatives on a open expanse containing \(S,\)
\[
{\color{silver} \int_a^b\int_c^d \operatorname{curl}\bm{F}\bigl(\bm{r}(s,t)\bigr)\cdot\bigl(\bm{r}_s\times\bm{r}_t\bigr) \,\mathrm{d}s\,\mathrm{d}t
=} \oiint_S \operatorname{curl}\bm{F} \cdot \mathbf{N} \,\mathrm{d}S
%= \oiint_S \operatorname{curl}\bm{F} \cdot \mathrm{d}\bm{S}
= \oint_{C} \bm{F}\cdot\mathrm{d}\bm{r}
{\color{silver} \;\;= \int_a^b \bm{F}\bigl(\bm{r}(t)\bigr)\cdot\bm{r}'(t) \,\mathrm{d}t}
%= \oint_{C} \bm{F}\cdot\bm{T} \,\mathrm{d}s
\,.
\]
I.e. the surface integral that computes the total circulation, the sum of the curl, on a surface
is equal to the line integral that computes the circulation along its boundary.
Stokes’ Theorem
(or the Kelvin-Stokes Theorem,
or the Curl Theorem) —
for an oriented piecewise-smooth surface \(S\) whose boundary \(C = \partial S\)
is a simple, closed, piecewise-smooth, positively-oriented curve,
and a vector field \(\bm{F}\) whose components
have continuous partial derivatives on a open expanse containing \(S,\)
\[
{\color{silver} \int_a^b\int_c^d \operatorname{curl}\bm{F}\bigl(\bm{r}(s,t)\bigr)\cdot\bigl(\bm{r}_s\times\bm{r}_t\bigr) \,\mathrm{d}s\,\mathrm{d}t
=} \oiint_S \operatorname{curl}\bm{F} \cdot \mathbf{N} \,\mathrm{d}S
%= \oiint_S \operatorname{curl}\bm{F} \cdot \mathrm{d}\bm{S}
= \oint_{C} \bm{F}\cdot\mathrm{d}\bm{r}
{\color{silver} \;\;= \int_a^b \bm{F}\bigl(\bm{r}(t)\bigr)\cdot\bm{r}'(t) \,\mathrm{d}t}
%= \oint_{C} \bm{F}\cdot\bm{T} \,\mathrm{d}s
\,.
\]
I.e. the surface integral that computes the total circulation, the sum of the curl, on a surface
is equal to the line integral that computes the circulation along its boundary.
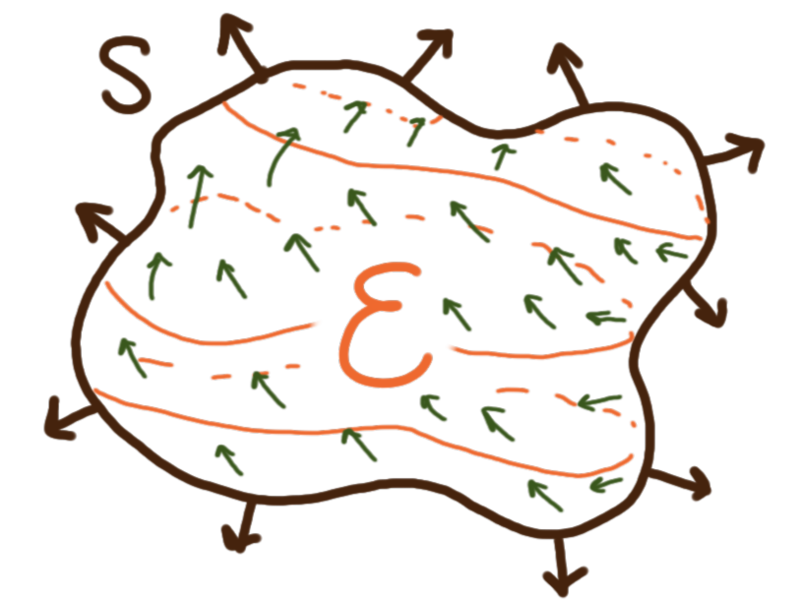 The Divergence Theorem
(or Gauss’s Theorem,
or Ostrogradsky’s Theorem) —
for a simple expanse \(E\) whose boundary \(S = \partial E\)
is a simple, closed, piecewise-smooth, and positively-oriented (outward) surface,
and for a vector field \(\bm{F}\) whose components
have continuous partial derivatives on a open expanse containing \(E,\)
\[
%{\color{silver} \int\limits_a^b\int\limits_{h_1(x)}^{h_2(x)}\int\limits_{g_1(x,y)}^{g_2(x,y)} \operatorname{div}F(x,y,z) \,\mathrm{d}z\,\mathrm{d}y\,\mathrm{d}x = }
\iiint_E \operatorname{div}\bm{F} \,\mathrm{d}V
= \oiint_{S} \bm{F}\cdot\mathrm{d}\bm{S}
{= \color{silver} \int_a^b\int_c^d \bm{F}\bigl(\bm{r}(s,t)\bigr)\cdot\bigl(\bm{r}_s\times\bm{r}_t\bigr) \,\mathrm{d}s\,\mathrm{d}t}
\,.
\]
I.e. the integral that computes the sum total of the divergence within an expanse
is equal to the surface integral across its boundary, the flux.
The Divergence Theorem
(or Gauss’s Theorem,
or Ostrogradsky’s Theorem) —
for a simple expanse \(E\) whose boundary \(S = \partial E\)
is a simple, closed, piecewise-smooth, and positively-oriented (outward) surface,
and for a vector field \(\bm{F}\) whose components
have continuous partial derivatives on a open expanse containing \(E,\)
\[
%{\color{silver} \int\limits_a^b\int\limits_{h_1(x)}^{h_2(x)}\int\limits_{g_1(x,y)}^{g_2(x,y)} \operatorname{div}F(x,y,z) \,\mathrm{d}z\,\mathrm{d}y\,\mathrm{d}x = }
\iiint_E \operatorname{div}\bm{F} \,\mathrm{d}V
= \oiint_{S} \bm{F}\cdot\mathrm{d}\bm{S}
{= \color{silver} \int_a^b\int_c^d \bm{F}\bigl(\bm{r}(s,t)\bigr)\cdot\bigl(\bm{r}_s\times\bm{r}_t\bigr) \,\mathrm{d}s\,\mathrm{d}t}
\,.
\]
I.e. the integral that computes the sum total of the divergence within an expanse
is equal to the surface integral across its boundary, the flux.