For a two-variable function \(f \colon \mathbf{R}^2 \to \mathbf{R}\) we say that the limit of \(f(x,y)\) as \((x,y)\) approaches \((a,b)\) is equal to \(L,\) denoted \(\lim_{(x,y) \to (a,b)} f(x,y) = L,\) if for every neighborhood of \(L\) there exists a neighborhood of \((a,b)\) such that for all \((x,y)\) in that neighborhood of \((a,b),\) \(f(x,y)\) will be in that neighborhood of \(L.\) The definition of continuity in this multivariable context is the same as the single-variable definition: a function \(f\) is continuous at a point \((a,b)\) if \(\lim_{(x,y) \to (a,b)} f(x,y) = f(a,b),\) and is continuous on its domain if it’s continuous at every point in its domain.
 When determining the limit of a single-variable function
there are only two directions from which to approach a point:
from the left and from the right.
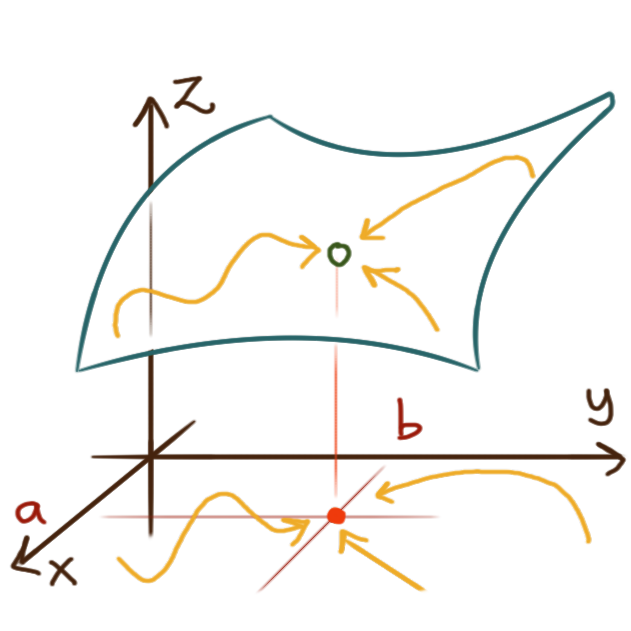
However for a multivariable function
there are infinitely many directions from which to approach a point.
A limit of a two-variable function only exists at \((a,b)\)
when the limit along any path
approaching the point \((a,b)\) exists
and the value of that limit is the same for any path.
To prove that a limit doesn’t exist
we can simply exhibit two paths in the domain approaching \((a,b)\)
along which the values of the limits differ.
To prove that a limit does exist
it’s often more convenient to transform space
by first centering the limit point \((a,b)\) at the origin
and then by converting to polar coordinates.
We can then consider if the single-variable limit as \(r\) approaches zero exists
irrespective of \(\theta.\)
When determining the limit of a single-variable function
there are only two directions from which to approach a point:
from the left and from the right.
However for a multivariable function
there are infinitely many directions from which to approach a point.
A limit of a two-variable function only exists at \((a,b)\)
when the limit along any path
approaching the point \((a,b)\) exists
and the value of that limit is the same for any path.
To prove that a limit doesn’t exist
we can simply exhibit two paths in the domain approaching \((a,b)\)
along which the values of the limits differ.
To prove that a limit does exist
it’s often more convenient to transform space
by first centering the limit point \((a,b)\) at the origin
and then by converting to polar coordinates.
We can then consider if the single-variable limit as \(r\) approaches zero exists
irrespective of \(\theta.\)