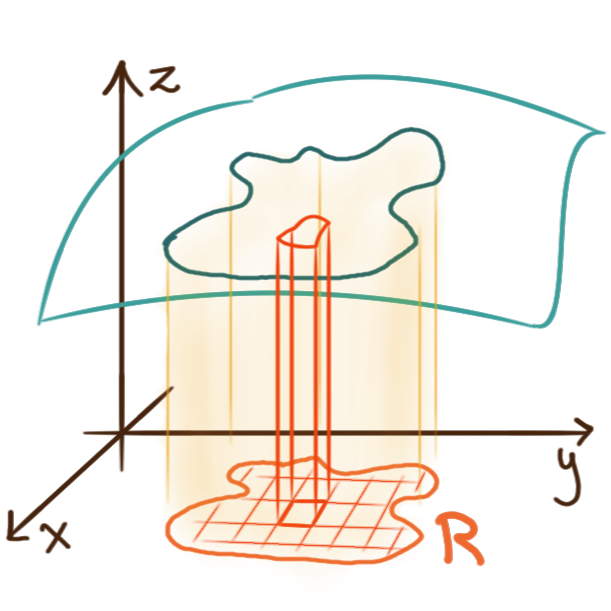
For a region \(R\) in the plane \(\mathbf{R}^2\)
and a function \(f\colon R \to \mathbf{R}\)
we define the double integral \(\iint_R f \,\mathrm{d}A\)
as a two-dimensional Riemann sum over a uniformly random sample
of points \(\{(x_{ij}^\ast, y_{ij}^\ast)\}\) within \(R:\)
\[
\iint_R f \,\mathrm{d}A
\;\;=\;\;
\lim_{\substack{\\[-3pt] m \to \infty \\[2pt] n \to \infty}} \sum_{j=1}^{n} \sum_{i=1}^{m} f\bigl(x_{ij}^\ast, y_{ij}^\ast\bigr) \,\mathrm{\Delta}A
\]
The differentials \(\mathrm{d}A\) and \(\Delta A\) represent “small changes in area”.
This integral computes the signed volume of the expanse
between the graph of \(f\) and the region \(R\).
Alternatively, thinking of \(R\) as a flat plate of some material with “density” function \(f\)
the integral can be interpreted as computing the “mass” of \(R.\)
In particular \(\iint_R 1 \,\mathrm{d}A\) computes the area of the region \(R\)
— the area of a region is the same as its mass if its density is uniformly \(1.\)
The average value of \(f\) over a region \(R\) is
\( \tfrac{1}{\operatorname{Area}(R)}\iint_R f \,\mathrm{d}A.\)
For an expanse \(E\) in three-dimensional space \(\mathbf{R}^3\) and a function \(f\colon E \to \mathbf{R}\) we define the triple integral \(\iiint_E f \,\mathrm{d}V\) as a Riemann sum: \[ \iiint_E f \,\mathrm{d}V \;\;=\;\; \lim_{\substack{\\[-4pt] \ell \to \infty \\[0pt] m \to \infty \\[0pt] n \to \infty }} \sum_{k=1}^{n} \sum_{j=1}^{m} \sum_{i=1}^{\ell} f\bigl(x_{ijk}^\ast, y_{ijk}^\ast, z_{ijk}^\ast\bigr) \,\mathrm{\Delta}V \] This integral computes a signed hypervolume, or alternatively, thinking of \(E\) as a chunk of material with density function \(f\) the integral can be interpreted as computing the mass of \(E.\) In particular \(\iiint_E 1 \,\mathrm{d}V\) computes the volume of the expanse \(E\) — the volume of an expanse is the same as its mass if its density is uniformly \(1.\)