 The gradient vector of a multivariable function \(f,\)
denoted either \(\operatorname{grad}f\) or \(\nabla f\),
(read as “del \(f,”\) even though the symbol \(\nabla\) is referred to as “nabla”),
is the vector of the partial derivatives of \(f.\)
The gradient is the “full” derivative of a multivariable function,
in contrast to its components which are just “partial” derivatives.
In two variables:
\[
\operatorname{grad}f
= \nabla f
= \Big\langle f_x, f_y \Big\rangle
= \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j}
\qquad\quad
\nabla f(x,y)
= \Big\langle f_x(x,y), f_y(x,y) \Big\rangle
\]
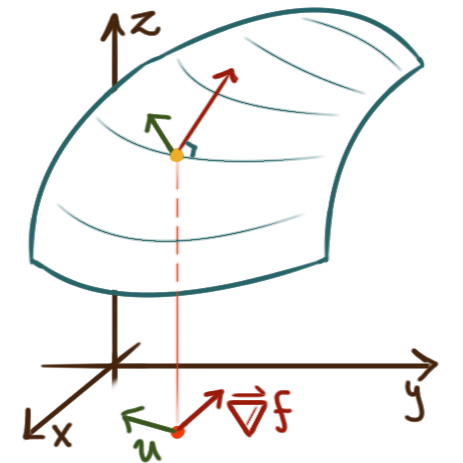
Note \(\nabla f\) is a vector in the domain of \(f,\)
not on the graph of \(f.\)
On the contour plot of \(f\) at a point \((a,b),\)
the vector \(\nabla f(a,b)\) will be perpendicular
to the level curve of \(f\) containing \((a,b).\)
On the graph \({z = f(x,y)}\) at the point \(\bigl(a,b, f(a,b)\bigr),\)
the vector \(\nabla f(a,b)\) will point in the direction
in which \(f\) is increasing the most
— the direction in which the tangent plane at the point is steepest —
and this maximal rate of increase will be \(\bigl|\nabla f(a,b)\bigr|.\)
The gradient vector of a multivariable function \(f,\)
denoted either \(\operatorname{grad}f\) or \(\nabla f\),
(read as “del \(f,”\) even though the symbol \(\nabla\) is referred to as “nabla”),
is the vector of the partial derivatives of \(f.\)
The gradient is the “full” derivative of a multivariable function,
in contrast to its components which are just “partial” derivatives.
In two variables:
\[
\operatorname{grad}f
= \nabla f
= \Big\langle f_x, f_y \Big\rangle
= \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j}
\qquad\quad
\nabla f(x,y)
= \Big\langle f_x(x,y), f_y(x,y) \Big\rangle
\]
Note \(\nabla f\) is a vector in the domain of \(f,\)
not on the graph of \(f.\)
On the contour plot of \(f\) at a point \((a,b),\)
the vector \(\nabla f(a,b)\) will be perpendicular
to the level curve of \(f\) containing \((a,b).\)
On the graph \({z = f(x,y)}\) at the point \(\bigl(a,b, f(a,b)\bigr),\)
the vector \(\nabla f(a,b)\) will point in the direction
in which \(f\) is increasing the most
— the direction in which the tangent plane at the point is steepest —
and this maximal rate of increase will be \(\bigl|\nabla f(a,b)\bigr|.\)
For a differentiable function \(f\) and a unit vector \(\bm{\hat{u}}\) in the domain of \(f,\) the directional derivative of \(f\) in the direction \(\bm{\hat{u}},\) denoted \(\operatorname{D}_{\bm{\hat{u}}} f\), is the function \(\nabla f \cdot \bm{\hat{u}}.\) Then for a point \((a,b)\) in the domain of \(f,\) the directional derivative \(\operatorname{D}_{\bm{\hat{u}}} f(a,b)\) will give the rate at which \(f\) is increasing (or decreasing) at the point \((a,b)\) in the direction \(\bm{\hat{u}}\) — it’s the “slope” on the graph of \(f\) in the direction of \(\bm{\hat{u}}.\) Because \(\bm{\hat{u}}\) is a unit vector, \(\operatorname{D}_{\bm{\hat{u}}} f(a,b)\) is just \(\bigl|\operatorname{proj}_{\bm{\hat{u}}}\bigl(\nabla f(a,b)\bigr)\bigr|.\) If \(\theta\) is the angle between \(\nabla f(a,b)\) and \(\bm{\hat{u}}\) then \(\operatorname{D}_{\bm{\hat{u}}} f(a,b) = \bigl|\nabla f(a,b)\bigr|\cos(\theta).\)
The gradient of a multivariable function \(f\colon \mathbf{R}^3 \to \mathbf{R}\) is \(\nabla f(x,y,z) = \big\langle f_x(x,y,z), f_y(x,y,z), f_z(x,y,z) \big\rangle\) as one would expect.