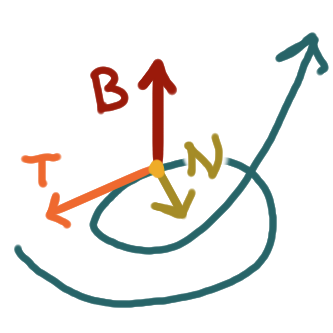
 For a smooth curve with smooth parameterization \(\bm{r},\)
at any position \(\bm{r}(t)\) the unit tangent vector \(\mathbf{T}(t)\)
is the unit vector pointing in the tangential direction,
parallel to \(\bm{r}'(t),\) to the curve at that point.
Since \(\mathbf{T}\) is a unit vector, it’ll be orthogonal to its derivative \(\mathbf{T}'.\)
The unit normal vector \(\mathbf{N}(t)\)
is the unit vector in the direction of \(\mathbf{T}'(t)\)
which points in the direction the curve is “curving” at that point.
Orthogonal to both \(\mathbf{T}(t)\) and \(\mathbf{N}(t)\)
is the unit binormal vector \(\mathbf{B}(t)\)
which points in the direction the curve is “twisting” at that point.
Altogether, these three vectors constitute the Frenet-Serret frame,
or TNB frame, of a curve at a point.
Explicitly these vectors can be calculated as:
\[
\displaystyle \mathbf{T} = \frac{\bm{r}'}{\bigl|\bm{r}'\bigr|}
\qquad \qquad
\displaystyle \mathbf{N} = \frac{\mathbf{T}'}{\bigl|\mathbf{T}'\bigr|}
\qquad \qquad
\displaystyle \mathbf{B} = \mathbf{T} \times \mathbf{N}
\]
Altogether, the Frenet-Serret frame provides a basis for
a local coordinate system relative to the point (a particle)
moving along the curve that respects the direction it’s going \(\mathbf{T},\)
the direction it’s “curving” \(\mathbf{N},\) and the direction it’s “twisting” \(\mathbf{B}.\)
This is as opposed to the absolute coordinate system
defined by the basis vectors
\(\mathbf{i}\) and \(\mathbf{j}\) and \(\mathbf{k}.\)
For a smooth curve with smooth parameterization \(\bm{r},\)
at any position \(\bm{r}(t)\) the unit tangent vector \(\mathbf{T}(t)\)
is the unit vector pointing in the tangential direction,
parallel to \(\bm{r}'(t),\) to the curve at that point.
Since \(\mathbf{T}\) is a unit vector, it’ll be orthogonal to its derivative \(\mathbf{T}'.\)
The unit normal vector \(\mathbf{N}(t)\)
is the unit vector in the direction of \(\mathbf{T}'(t)\)
which points in the direction the curve is “curving” at that point.
Orthogonal to both \(\mathbf{T}(t)\) and \(\mathbf{N}(t)\)
is the unit binormal vector \(\mathbf{B}(t)\)
which points in the direction the curve is “twisting” at that point.
Altogether, these three vectors constitute the Frenet-Serret frame,
or TNB frame, of a curve at a point.
Explicitly these vectors can be calculated as:
\[
\displaystyle \mathbf{T} = \frac{\bm{r}'}{\bigl|\bm{r}'\bigr|}
\qquad \qquad
\displaystyle \mathbf{N} = \frac{\mathbf{T}'}{\bigl|\mathbf{T}'\bigr|}
\qquad \qquad
\displaystyle \mathbf{B} = \mathbf{T} \times \mathbf{N}
\]
Altogether, the Frenet-Serret frame provides a basis for
a local coordinate system relative to the point (a particle)
moving along the curve that respects the direction it’s going \(\mathbf{T},\)
the direction it’s “curving” \(\mathbf{N},\) and the direction it’s “twisting” \(\mathbf{B}.\)
This is as opposed to the absolute coordinate system
defined by the basis vectors
\(\mathbf{i}\) and \(\mathbf{j}\) and \(\mathbf{k}.\)
 The plane spanned by \(\mathbf{T}\) and \(\mathbf{N}\)
is called the osculating plane.
Similarly the plane spanned by \(\mathbf{N}\) and \(\mathbf{B}\)
is called the normal plane and the tangential direction of the curve is normal to this plane.
The plane spanned by \(\mathbf{T}\) and \(\mathbf{B}\)
is called the rectifying plane.
The acceleration vector \(\bm{\alpha}\) always lies in the osculating plane,
and can be resolved in terms of the unit tangent and normal vectors as
\[\bm{\alpha} = |\bm{v}|'\mathbf{T}+|\bm{v}||\mathbf{T}'|\mathbf{N}\,.\]
The plane spanned by \(\mathbf{T}\) and \(\mathbf{N}\)
is called the osculating plane.
Similarly the plane spanned by \(\mathbf{N}\) and \(\mathbf{B}\)
is called the normal plane and the tangential direction of the curve is normal to this plane.
The plane spanned by \(\mathbf{T}\) and \(\mathbf{B}\)
is called the rectifying plane.
The acceleration vector \(\bm{\alpha}\) always lies in the osculating plane,
and can be resolved in terms of the unit tangent and normal vectors as
\[\bm{\alpha} = |\bm{v}|'\mathbf{T}+|\bm{v}||\mathbf{T}'|\mathbf{N}\,.\]