A force \(\bm{F}\), having a direction and magnitude (measured in Newtons), can be modelled by as vector. The resultant (net) force on a mass is the sum of all the individual component forces acting on that mass. The work \(W\) done by a force acting on an object is the (scalar) amount of force accumulated as the object is displaced. For a constant force \(\bm{F}\) vector with magnitude \(|\bm{F}|\) and displacement vector \(\bm{s}\) with magnitude \(|\bm{s}|\) the work done by that force in the direction of \(\bm{s}\) is the magnitude of the component of the projection of \(\bm{F}\) onto \(\bm{s}.\) I.e \( {W = \big(|\bm{F}|\cos(\theta)\big)|\bm{s}| = \bm{F}\cdot\bm{s}\,.}\) Much more generally, if the force \(\bm{F}\) is not constant but instead a function of time \(t,\) and if the displacement is not in a single direction but instead directed along some curve \(C\) in space, the work accumulated must be computed as an (line) integral: \[ W = \int\limits_C \bm{F} \cdot \mathrm{d}\bm{s} = \int\limits_{\Delta t} \bm{F}(t) \cdot \frac{\mathrm{d}\bm{s}}{\mathrm{d}t} \,\mathrm{d}t\,. \] The integrand \(\bm{F}(t) \cdot \frac{\mathrm{d}\bm{s}}{\mathrm{d}t}\,,\) the dot product of the force vector with the velocity vector, the rate at which work is being done, is called the power of the force. Per the fundamental theorem of calculus, power then is the derivative of work over time: \( P = \dot{W}\,.\)
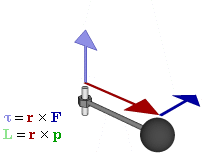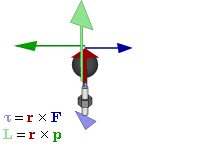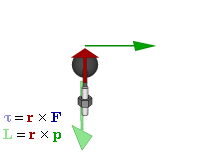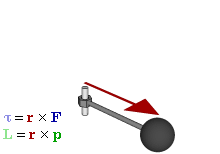 Torque, a vector, the rotational analogue of linear force,
measures the tendency of a body to rotate about the origin.
For example, if the direction of the wrench is described by a (radial) vector \(\bm{r}\)
and a force \(\bm{F}\) is applied to turn the wrench,
the torque is \(\bm{\tau} = \bm{r} \times \bm{F}\,.\)
Just like torque is the rotational analogue of linear force,
angular momentum \(\bm{L}\) is the rotational analogue of momentum \(\bm{p} = m\bm{v},\)
where \(m\) is mass and \(\bm{v}\) is the velocity vector.
In general, the result of weighting a physical quantity by its position \(\bm{r}\)
is referred to as the first moment of that quantity.
Torque is the first moment of (linear) force,
and angular momentum is the first moment of momentum.
Torque, a vector, the rotational analogue of linear force,
measures the tendency of a body to rotate about the origin.
For example, if the direction of the wrench is described by a (radial) vector \(\bm{r}\)
and a force \(\bm{F}\) is applied to turn the wrench,
the torque is \(\bm{\tau} = \bm{r} \times \bm{F}\,.\)
Just like torque is the rotational analogue of linear force,
angular momentum \(\bm{L}\) is the rotational analogue of momentum \(\bm{p} = m\bm{v},\)
where \(m\) is mass and \(\bm{v}\) is the velocity vector.
In general, the result of weighting a physical quantity by its position \(\bm{r}\)
is referred to as the first moment of that quantity.
Torque is the first moment of (linear) force,
and angular momentum is the first moment of momentum.