For a rectangular region \(R = [a,b] \times [c,d]\) in \(\mathbf{R}^2\) and a function \(f\colon R \to \mathbf{R},\) the double integral \(\iint_R f \,\mathrm{d}A\) is equal to an iterated integral that can be evaluated “one variable at a time” by applying the fundamental theorem of calculus twice. \[ \iint\limits_R f \,\mathrm{d}A \;\;=\;\; \int\limits_a^b\left(\int\limits_c^d f(x,y) \,\mathrm{d}y\right)\mathrm{d}x \;\;=\;\; \int\limits_a^b\int\limits_c^d f(x,y) \,\mathrm{d}y\,\mathrm{d}x \] But we may integrate in the opposite order too. Fubini’s Theorem, an analogue to Clairaut’s Theorem for integration, states that if \(f\) is continuous on the rectangle \(R = [a,b] \times [c,d]\) then we have equality \( {\int_a^b\int_c^d f(x,y) \,\mathrm{d}y\,\mathrm{d}x = \int_c^d\int_a^b f(x,y) \,\mathrm{d}x\,\mathrm{d}y.} \)
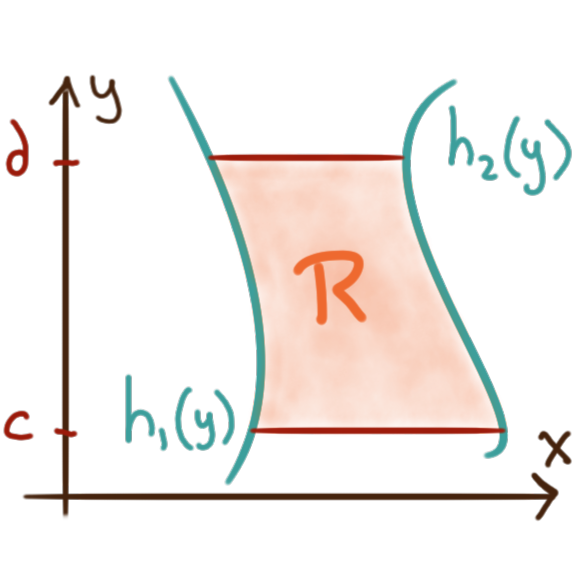
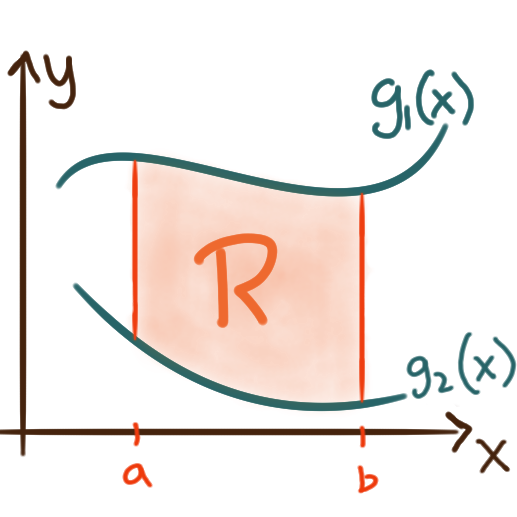 If \(R\) is not rectangular, but does have a boundary
that can be described analytically as, for example, the graphs of functions
\({y=g_1(x)}\) and \({y=g_2(x),}\) or as \({x=h_1(y)}\) and \({x=h_2(y),}\)
then the double integral \(\iint_R f \,\mathrm{d}A\) can be be computed respectively as:
\[
\int\limits_a^b\int\limits_{g_1(x)}^{g_2(x)} f(x,y) \,\mathrm{d}y\,\mathrm{d}x
\quad\text{or}\quad
\int\limits_c^d\int\limits_{h_1(y)}^{h_2(y)} f(x,y) \,\mathrm{d}x\,\mathrm{d}y
\]
If \(R\) is not rectangular, but does have a boundary
that can be described analytically as, for example, the graphs of functions
\({y=g_1(x)}\) and \({y=g_2(x),}\) or as \({x=h_1(y)}\) and \({x=h_2(y),}\)
then the double integral \(\iint_R f \,\mathrm{d}A\) can be be computed respectively as:
\[
\int\limits_a^b\int\limits_{g_1(x)}^{g_2(x)} f(x,y) \,\mathrm{d}y\,\mathrm{d}x
\quad\text{or}\quad
\int\limits_c^d\int\limits_{h_1(y)}^{h_2(y)} f(x,y) \,\mathrm{d}x\,\mathrm{d}y
\]
The surface area of the portion of the graph \(z \!=\! f(x,y)\) above a region \(R\) is given by the integral \( \iint_{R} \sqrt{ \bigl(f_x(x,y)\bigr)^2 \!+\! \bigl(f_y(x,y)\bigr)^2 \!+\! \bigl(1\bigr)^2 } \,\,\mathrm{d}A \,.\)