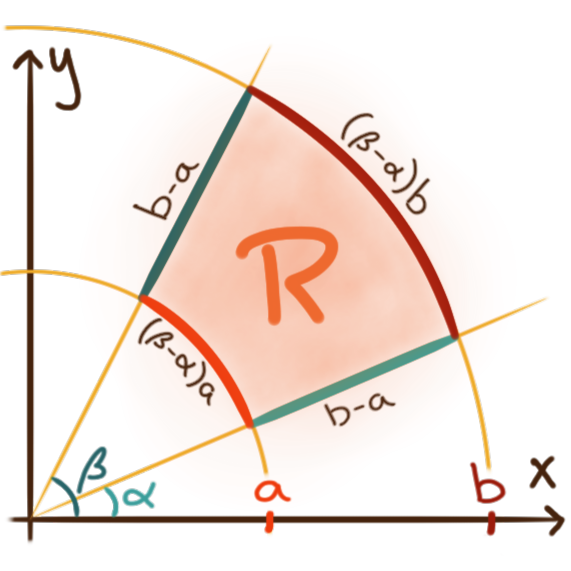
 Recall that a point in the plane \(\mathbf{R}^2\) with rectangular (Cartesian) coordinates \((x,y)\)
can be expressed in polar coordinates as \(\bigl(\sqrt{x^2+y^2}, \operatorname{atan2}(y,x)\bigr).\)
A polar “rectangle” in \(\mathbf{R}^2\) is a region
at the intersection of two circular sectors of radii \(a\) and \(b\) respectively
bound between two angles \(\alpha\) and \(\beta.\)
For such a polar rectangle region \(R\) the double integral of \(f\) over \(R\)
can be calculated as an iterated integral
with an additional integrating factor of \({\color{maroon} r}\)
to correct for the scaling of a polar rectangle’s area
depending on its distance \(r\) from the origin.
\[
\iint\limits_{R} f(x,y) \,\mathrm{d}A
\;\;= \;\;
\int\limits_\alpha^\beta \int\limits_a^b f\bigl(r\cos(\theta),r\sin(\theta)\bigr) \,{\color{maroon} r} \,\mathrm{d}r\,\mathrm{d}\theta
\]
Recall that a point in the plane \(\mathbf{R}^2\) with rectangular (Cartesian) coordinates \((x,y)\)
can be expressed in polar coordinates as \(\bigl(\sqrt{x^2+y^2}, \operatorname{atan2}(y,x)\bigr).\)
A polar “rectangle” in \(\mathbf{R}^2\) is a region
at the intersection of two circular sectors of radii \(a\) and \(b\) respectively
bound between two angles \(\alpha\) and \(\beta.\)
For such a polar rectangle region \(R\) the double integral of \(f\) over \(R\)
can be calculated as an iterated integral
with an additional integrating factor of \({\color{maroon} r}\)
to correct for the scaling of a polar rectangle’s area
depending on its distance \(r\) from the origin.
\[
\iint\limits_{R} f(x,y) \,\mathrm{d}A
\;\;= \;\;
\int\limits_\alpha^\beta \int\limits_a^b f\bigl(r\cos(\theta),r\sin(\theta)\bigr) \,{\color{maroon} r} \,\mathrm{d}r\,\mathrm{d}\theta
\]
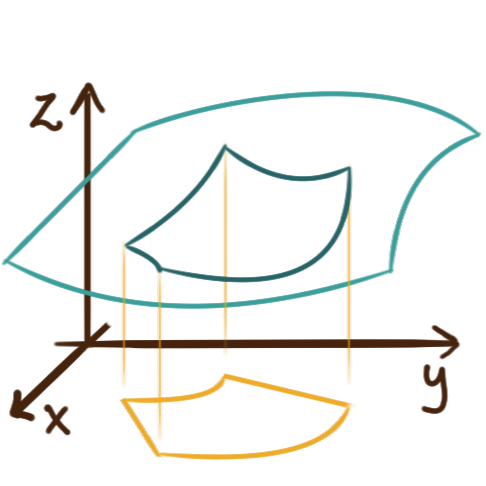 This integral computes the signed volume of the expanse
bound between the graph \({z = f(x,y)}\) and the region \(R\) in the \(xy\)-plane.
Alternatively, thinking of \(f\) as a “density” function on \(R\)
the integral can be interpreted as computing the “mass” of \(R.\)
If the “inner radius” and “outer radius” of the region \(R\) are not constant
but are instead given analytically as functions \(h_1(\theta)\) and \(h_2(\theta),\)
the double integral of \(f\) over \(R\) can be computed as
\[\int\limits_\alpha^\beta \int\limits_{h_1(\theta)}^{h_2(\theta)} f\bigl(r\cos(\theta),r\sin(\theta)\bigr) \,{\color{maroon} r} \,\mathrm{d}r\,\mathrm{d}\theta\,.\]
This integral computes the signed volume of the expanse
bound between the graph \({z = f(x,y)}\) and the region \(R\) in the \(xy\)-plane.
Alternatively, thinking of \(f\) as a “density” function on \(R\)
the integral can be interpreted as computing the “mass” of \(R.\)
If the “inner radius” and “outer radius” of the region \(R\) are not constant
but are instead given analytically as functions \(h_1(\theta)\) and \(h_2(\theta),\)
the double integral of \(f\) over \(R\) can be computed as
\[\int\limits_\alpha^\beta \int\limits_{h_1(\theta)}^{h_2(\theta)} f\bigl(r\cos(\theta),r\sin(\theta)\bigr) \,{\color{maroon} r} \,\mathrm{d}r\,\mathrm{d}\theta\,.\]