Given two vectors \(\bm{u} = \langle u_1,u_2,u_3 \rangle\) and \(\bm{v} = \langle v_1,v_2,v_3 \rangle,\) their dot product \(\bm{u}\cdot\bm{v}\) (sometimes called the scalar product or inner product) is the number defined as the result of the calculation \({\bm{u}\cdot\bm{v} = u_1 v_1 + u_2 v_2 + u_3 v_3.}\) Alternatively if \(\theta\) is the angle between \(\bm{u}\) and \(\bm{v},\) then \({\bm{u}\cdot\bm{v} = |\bm{u}||\bm{v}|\cos(\theta).}\) If two vectors are perpendicular (orthogonal) then \(\bm{u}\cdot\bm{v} = 0,\) and if two vectors are parallel then \(\bm{u}\cdot\bm{v} = |\bm{u}||\bm{v}|.\) Intuitively then, the dot product is the product of the magnitudes of two vectors “correcting for” how much they aren’t pointing in the same direction. Notably, by that characterization of the dot product in terms of cosine, given two vectors \(\bm{u}\) and \(\bm{v},\) the measure of the angle \(\theta\) between them is given by the formula \(\theta = \arccos\bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{u}||\bm{v}|}\bigr)\,.\)
The dot product is a commutative product: \(\bm{u}\cdot\bm{v}=\bm{v}\cdot\bm{u}.\) For two vectors \(\bm{u} = \langle u_1,u_2,u_3 \rangle\) and \(\bm{v} = \langle v_1,v_2,v_3 \rangle,\) and a scalar (constant) \(c\) we have \({c(\bm{u}\cdot\bm{v})=(c\bm{v})\cdot\bm{u}=\bm{v}\cdot(c\bm{u}).}\)
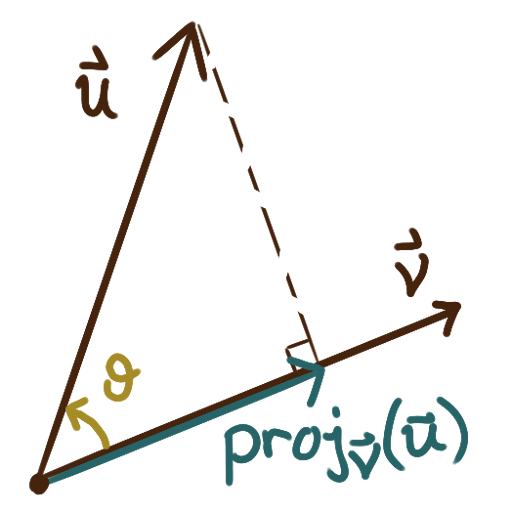 The projection of \(\bm{u}\) onto \(\bm{v}\) (a vector),
denoted \(\operatorname{proj}_{\bm{v}}(\bm{u}),\)
is calculated as
\[
\operatorname{proj}_{\bm{v}}(\bm{u})
= \bigl(|\bm{u}|\cos(\theta)\bigr)\bm{\hat{v} }
= \Bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{v}|}\Bigr)\bm{\hat{v}}
= \Bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{v}|^2}\Bigr)\bm{v}
\]
Imagine a light shines directly down, perpendicularly, onto \(\bm{v};\)
\(\operatorname{proj}_{\bm{v}}(\bm{u})\) is the “shadow” that \(\bm{u}\) casts onto \(\bm{v}.\)
The component of \(\bm{u}\) along \(\bm{v}\) (a number)
is the length of the projection of \(\bm{u}\) onto \(\bm{v},\) i.e.
\[
\bigl|\operatorname{proj}_{\bm{v}}(\bm{u})\bigr|
= |\bm{u}|\cos(\theta)
= \frac{|\bm{u}\cdot\bm{v}|}{|\bm{v}|}
\]
The projection of \(\bm{u}\) onto \(\bm{v}\) (a vector),
denoted \(\operatorname{proj}_{\bm{v}}(\bm{u}),\)
is calculated as
\[
\operatorname{proj}_{\bm{v}}(\bm{u})
= \bigl(|\bm{u}|\cos(\theta)\bigr)\bm{\hat{v} }
= \Bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{v}|}\Bigr)\bm{\hat{v}}
= \Bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{v}|^2}\Bigr)\bm{v}
\]
Imagine a light shines directly down, perpendicularly, onto \(\bm{v};\)
\(\operatorname{proj}_{\bm{v}}(\bm{u})\) is the “shadow” that \(\bm{u}\) casts onto \(\bm{v}.\)
The component of \(\bm{u}\) along \(\bm{v}\) (a number)
is the length of the projection of \(\bm{u}\) onto \(\bm{v},\) i.e.
\[
\bigl|\operatorname{proj}_{\bm{v}}(\bm{u})\bigr|
= |\bm{u}|\cos(\theta)
= \frac{|\bm{u}\cdot\bm{v}|}{|\bm{v}|}
\]