Integration by Substitution
& Areas Between Curves

  1. Evaluate as many of these indefinite integrals as you need to feel confident with the technique of substitution (change of coordinates). Aim to be not just familiar, but adept at this skill. Don’t forget your \(+C\)s!
    \(\displaystyle\int \sqrt{3x-7} \,\mathrm{d}x\)
    \(\displaystyle\int \frac 1 2 \sec^2(3x-7) \,\mathrm{d}x\)
    \(\displaystyle\int \frac{\mathrm{d}x}{(3x-7)^2} \)
    \(\displaystyle\int \cos(7x) \,\mathrm{d}x\)
    \(\displaystyle\int x\cos\!\big(7x^2\big) \,\mathrm{d}x\)
    \(\displaystyle\int x^3\cos\!\left(7x^4\right) \,\mathrm{d}x\)
    \(\displaystyle\int \cos(x)\cos\!\big(\sin(x)\big) \,\mathrm{d}x\)
    \(\displaystyle\int \sin(x)\cos^{9}(x) \,\mathrm{d}x\)
    \(\displaystyle\int x\sqrt{3x-7} \,\mathrm{d}x\)
    \(\displaystyle\int \frac{1+\cot^2(x)}{(1+\cot(x))^2} \,\mathrm{d}x\)
    \(\displaystyle\int \frac{\sin\left(\frac{1}{x^2}\right)}{x^3} \,\mathrm{d}x\)
    \(\displaystyle\int \sqrt{\tan(x)\sec^4(x)} \,\mathrm{d}x\)
  2. Can you evaluate these definite integrals?
    \(\displaystyle\int\limits_{1}^{3} \frac{\mathrm{d}x}{(3x-7)^2} \)
    \(\displaystyle\int\limits_{0}^{\sqrt{\pi/42}} x\cos\!\big(7x^2\big) \,\mathrm{d}x\)
    \(\displaystyle\int\limits_{0}^{1} x^3\left(x^2+1\right)^9 \,\mathrm{d}x\)
  3. Calculate the area of the region in the \(xy\)-plane enclosed between the curves given by the equations \(y=x^2\) and \(y=x+6.\)
  4. What’s the area of a single “hump” under the graph of sine?
  5. Consider the region enclosed by the curves \(y=x^2\) and \(y=x^3.\) Write two different integrals, one with respect to \(x\) and the other with respect to \(y,\) that represent the area of this region, then calculate the values of each of these integrals to verify they have the same value.
  6. What’s the area of the triangle in the \(xy\)-plane with vertices located at coordinates \((1,1),\) \((7,2),\) and \((5,8)?\) Bonus: look up and use Pick’s Theorem to verify your calculation.
  7. Calculate the area of the region in the \(xy\)-plane enclosed between the curves given by the equations \(y=\sqrt{x}\) and \(y=6-x\) and \(y=0.\) Protip: integrate with respect to \(y\) so you can set it up as a single integral.
  8. Calculate the area of the region in the \(xy\)-plane enclosed between the curves given by the equations \(y=\sec^2(x)\) and \(y=8\cos(x).\)
  9. The curves \(y=\sin(x)\) and \(y=\cos(x)\) enclose a region consisting of infinitely many repeating copies of a single shape. What’s the area of this shape?

  10. James Stewart

    There is a line through the origin that divides the region bounded by the parabola \(y=x-x^2\) and the \(x\)-axis into two regions with equal area. What is the slope of that line?

Challenges

  1. James Stewart

    Prove that if \(f\) is continuous, then \[ \int\limits_0^x f(u)(x-u)\,\mathrm{d}u \;\;=\;\; \int\limits_0^x \left(\int\limits_0^u f(t)\,\mathrm{d}t\right)\,\mathrm{d}u \] How can we interpret this equation geometrically?

  2. James Stewart

    If the tangent at a point \(P\) on the curve \(y = x^3\) intersects the curve again at \(Q\), let \(A\) be the area of the region bounded by the curve and the line segment \(PQ\). Let \(B\) be the area of the region defined in the same way starting with \(Q\) instead of \(P\). What is the relationship between \(A\) and \(B\)?

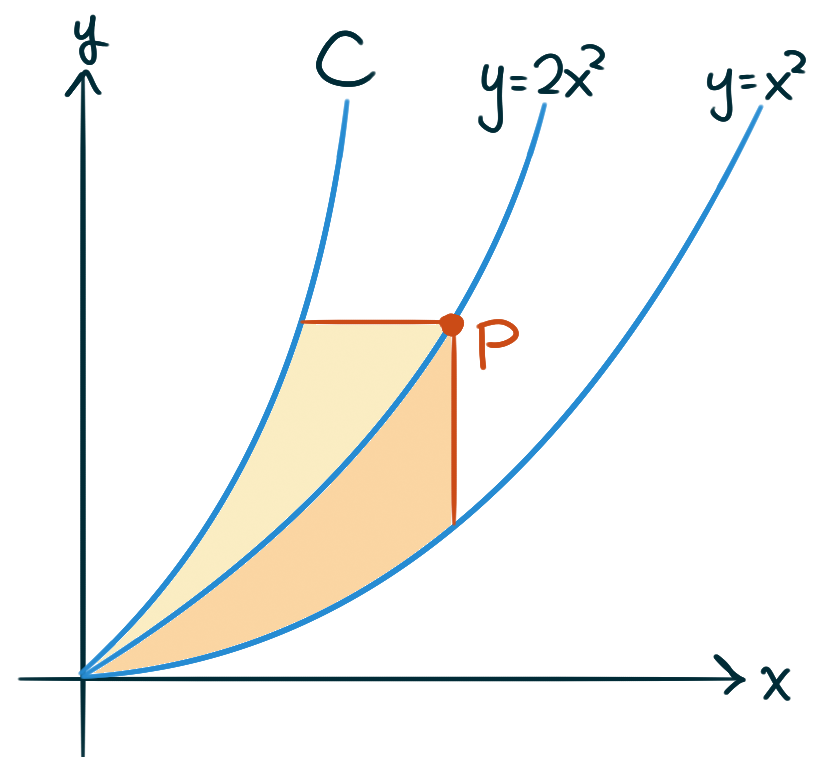
  3. James Stewart

    The figure shows three curves, \(y=x^2,\) \(y=2x^2,\) and \(C,\) such that for every point \(P\) on the middle curve \(y = 2x^2\), the shaded areas are equal. Find an equation for \(C\).