Optimization Problems & Newton's Method

What are the global extrema of this function on the interval $[-1,3]?$

$ \displaystyle f(x) = x^{3}-2x^{2}-x+2 $
What’s the minimum vertical distance between the graphs of $f$ and $g?$ (Desmos)

$f(x) = x^2+7x+5$

$g(x) = 2x-x^2$
What are two numbers whose difference is $42$ and whose product is minimal?
Suppose you want to build a rectangular, fenced-in pen along a river; this way you only need to build three sides of the pen. You have 420 ft of prefabricated fencing. What’s the maximum possible area of the plot you can enclose?
You must cut a 42 inch long length of copper wire into two pieces, bending one piece into a square and the other into a circle. Where do you cut the wire so that the total area of the square and the circle is maximized? Where do you cut the wire so that the total area of the square and the circle is minimized?
The Coca-Cola Company plans on cutting manufacturing costs. They want to redesign the shape of their 12 fl oz soda can to use as little aluminum as possible. What are the dimensions of a can that will achieve this?

For US food products, 1 fl oz ≈ 30 ml, which as a volume corresponds to 30 cm³.
What are the global extrema of this function on the interval $[0,4]?$

$ f(x) = x^3 - 7x^2 +14x -8 $
What’s the shortest vertical distance between these function’s graphs?

$ f(x) = 4-(x+1)^2 $

$ g(x) = (x-3)^2+2 $
If the sum of two positive numbers is 42, what is the minimum possible value of the sum of their squares?
What are the length and width of a rectangle with perimeter 420 ft whose area is maximal?
A farmer plans in building a rectangular fenced-in pen for his aardvarks and his badgers. The aardvarks and badgers shouldn’t mingle though (obviously), so the farmer plans on building another length of fencing along the diagonal of the pen to separate the aardvarks and badgers into two smaller equal-sized triangular pens. If the farmer has 420 ft of prefabricated fencing, what is the maximal area of pen he can build?
An open-top box is to be constructed from a square, 42″×42″ piece of cardboard, by cutting small squares from the corners of the cardboard and folding up and taping together the resulting “flaps” to be the sides of the box. What size squares should be cut from the corners to maximize the volume of the resulting box?
What are the dimensions, in terms of $r,$ of the rectangle of largest possible area that can be inscribed in a semicircle of radius $r$ where one side of the rectangle lies in the diameter of the semicircle.
A 42 ft³ closed-top box is to be manufactured with the following specifications: the length of the base of the box will be twice its width, the top and bottom of the box will be constructed out of carbon steel which costs $23 per square foot, the sides will be constructed out of galvanized steel which costs $17 per square foot, and all the sides will be welded together along the edges. What dimensions will minimize the cost to manufacture the box?
An closed-top box is to be constructed from a square, 42″×42″ piece of cardboard, by cutting squares and rectangles from the corners of the cardboard and folding up and taping together the resulting “flaps” to be the sides and lid of the box. What size squares and rectangles should be cut from the corners to maximize the volume of the resulting box?
Jungic, Menz, Pyke The top and bottom margins of a poster are each $6\mathrm{cm}$, and the side margins are each $4\mathrm{cm}$. If the area of the printed material on the poster (that is, the area between the margins) is fixed at $384\mathrm{cm}^2,$ find the dimensions of the poster with the smallest total area.
Jungic, Menz, Pyke A water trough — like a rain gutter — is to be made from a long strip of tin 8in wide by taking 3in on each side of that width and bending them up at and angle $\theta$. What angle $\theta$ would maximize the cross sectional area, and thus the amount of water, the trough holds?
Jungic, Menz, Pyke Maya is 2 km offshore in a boat and wishes to reach a coastal village which is 6 km down a straight shoreline from the point on the shore nearest to the boat. She can row at 2 km/hr and run at 5 km/hr. Where should she land her boat to reach the village in the least amount of time?
Jungic, Menz, Pyke A storage container is to be made in the form of a right circular cylinder with a volume of 287ft². Material for the top of the container costs $5 per square foot and material for the sides and base costs $2 per square foot. What dimensions will minimize the total cost of the container?
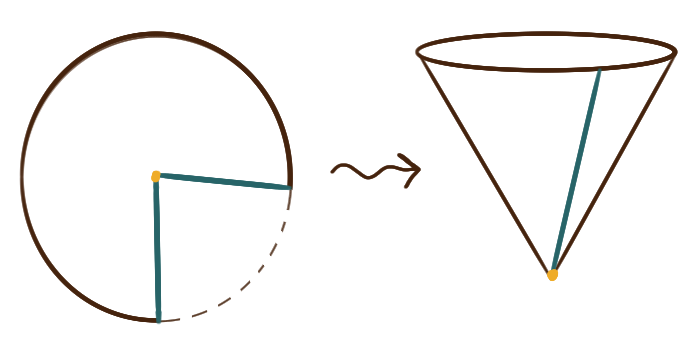A sector of a circle can be folded up into a cone. Some cheap water cups are constructed this way: start with a disk of waxed paper, make two cuts to remove a small sector of the disk, and adhere the disk along the two cuts to make a “cup”. (Obviously it’s more complicated than this; you need to leave a little paper tab to glue across the cut, but let’s keep this problem simple.) Suppose the initial circular sector has radius $r$ and has a subtended angle measuring $\theta.$ What angle $\theta$ corresponds to the cup that holds the maximal amount of water?
Using the fact that the vertex of a parabola is the location of its global minimum/maximum (depending on its orientation), show that the $x$-coordinate of the vertex of the parabola given by the graph of $f(x) = ax^2+bx+c$ is $\frac{-b}{2a}.$
A Norman window has a shape of a rectangle surmounted by a semicircle — it has three straight sides and one curved side on top, and the diameter of the semi-circular curved side is equal to the width of the rectangle.
1. If the perimeter of the window is fixed at 12 ft, what are the dimensions that result in the window having maximal area?
2. If the area of the window is fixed at 10 ft², what are the dimensions that result in the window having minimal perimeter?
openstax Two poles are connected by a wire that is also connected to the ground. The first pole is 20 ft tall and the second pole is 10 ft tall. There is a distance of 30 ft between the two poles. Where should the wire be anchored to the ground to minimize the amount of wire needed?
openstax A rectangle is to be inscribed in the ellipse \[\frac{x^2}{4} + \frac{y^2}{1} = 1\,.\] with its sides parallel and perpendicular to the coordinate axis — i.e. it’s not tilted. What should the dimensions of the rectangle be to maximize its area? What is the maximum area?
Dawkins A long steel pipe is being carried, perfectly level, down a hallway. The hallway is 15 ft wide, but makes an abrupt right-angled turn into a hallway that is only 6 ft wide. What is the longest the pipe could possibly be to make this turn while still being held perfectly level?
Jungic, Menz, Pyke With a straight piece of wire 4 m long, you are to create an equilateral triangle and a square, or either one only. Suppose a piece of length $x$ meters is bent into triangle and the reminder is bent into a square. Find the value of $x$ which maximizes the total area of both triangle and square.
What are the dimensions of an isosceles triangle inscribed in a circle of radius $r$ (with vertices on the boundary of the circle) that has maximal area?
Suppose one side of a triangle has length $\ell$ and another side has length $2\ell$. Show that he maximum possible area of the triangle is $\ell^2.$
Reinholz Find the equation of the line through the point $(2,4)$ that cuts off the least area from the first quadrant.
Jungic, Menz, Pyke For positive integers $m$ and $n,$ what is the maximum possible value of $f(x) = x^m(1-x)^n?$
James Stewart If the tangent line at a point $P$ on the curve $y = x^3$ intersects the curve again at $Q$, let $A$ be the area of the region bounded by the curve and the line segment $PQ.$ Let $B$ be the area of the region defined the same way but starting with $Q$ instead of $P.$ What is the relationship between $A$ and $B?$
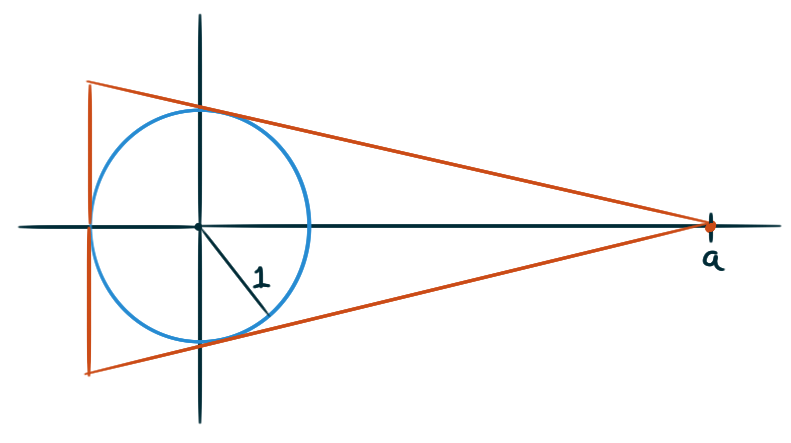James Stewart An isosceles triangle is circumscribed about a unit circle so that the equal sides meet at the point $(a,0)$ on the $x$-axis. Find the value of $a$ that minimizes the lengths of the equal sides.
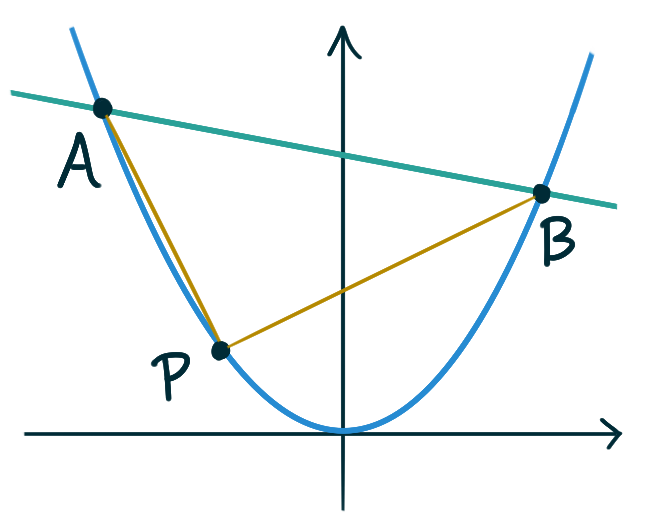James Stewart The line $y = mx + b$ intersects the parabola $y = x^2$ in points $A$ and $B$. Find the point $P$ on the arc the parabola that maximizes the area of the triangle $PAB$.
Consider the scenario from a previous question about carrying a long steel pipe around a corner. Suppose that the hallways were both 12 ft tall, and the pipe didn’t have to be held perfectly level. What is the longest the pipe could possibly be to make this turn?
In general, there is no explicit formula for the roots of polynomial of degree higher than four. However we can use Newton’s method to approximate the roots of any polynomial. Approximate the value of the single real root of this polynomial using Newton’s method. \[x^5 + 2x^4 + 3x^3 + 4x^2 + 5x +6\]
The arctangent function has a single root at zero. But, depending on the initial guess, Newton’s method might fail to hone in on this root, and will instead return numbers further and further away from zero. Graph the function $y = \arctan(x)$ and, based on the geometry of the graph, figure out for which initial guesses Newton’s method will converge to zero, and for which initial guesses Newton’s method will diverge.
The polynomial $x^3-x$ has three roots: $-1$ and $0$ and $1.$ Determine the set of all real numbers $x$ such that Newton’s method will converge to $1$ upon being initiated with guess $x$.
For any positive number $N,$ here is a simple method for approximating the square root of $N.$ Start by guessing/estimating some positive integer $x$ near $\sqrt{N}.$ Plugging $x$ into the formula \[x_\star = \frac{1}{2}\left(x + \frac{N}{x}\right)\] will result in a number $x_\star$ that is closer to $\sqrt{N}$ than $x.$ In fact, plugging any input into this formula will return a number closer to $\sqrt{N}$ than the input. Furthermore, the successive outputs that result from recursively applying this formula, plugging each output back in as the next input, will approach the exact value of $\sqrt{N}.$ This procedure is commonly called the Babylonian method for computing square roots since it was known to Babylonian mathematicians millennia ago.
1. Show that this formula is the same as the “next guess” formula that would result from applying Newton’s method to approximate a solution of the equation $x^2-N=0,$ hence justifying why this Babylonian method works.
2. Write a computer program that iteratively applies this formula to approximate the square root of a number accurate to the precision of your chosen language’s analogue of the float data type. Note: a TI-83/84+ calculator is programmable. Once you have an iterative program, see if you can alter it to make it recursive instead.
3. Come up with similar recursive formulas for the operations $\sqrt[3]{x} $ and $\frac{1}{x}\,. $
  
  It can be tough to figure out the one for $\frac{1}{x}$. The formula (procedure) you get for it though, called Newton-Raphson division, is rather noteworthy.
The equation $\cos(x) = x$ has a single solution. We call it the Dottie Number. (Recall that cosine expects its argument in radian measure.)
1. Calculating the Dottie number accurate to seven decimal places.
2. Write a program that performs Newton’s Method, and use that program to calculate the Dottie number accurate to the precision of your chosen language’s float data type. Note the TI-83/84+ series of calculators are programmable. Can your program calculate $x$ to arbitrary precision?
3. Take the cosine of any number. Then take the cosine of that result. And then take the cosine of that result. And then take the cosine of that result. Keep doing this for awhile, and you should notice that this process converges to that same solution to $\cos(x) = x$. Assuming this does converge, why must it converge to this same number?
Sometimes Newton’s method fails to converge, but not because the successive approximations blow up towards infinity.
1. Consider the polynomial $x^3-2x+2.$ This polynomial has a root at ${x \approx -1.7693.}$ However, applying Newton’s method, if we start with the initial guess at zero, the method will not converge to the root. Investigate why Newton’s method fails in this case. Are there any other initial guesses for which Newton’s method will fail to converge to the root?
2. Similarly, investigate $x^5-x-1$ with an initial guess of zero.
3. To ascribe vocabulary to the phenomenon in those previous examples, certain initial guesses $x_0$ may not lead to a sequence $x_1, x_2, \dotsc$ that converges to the root of the function, but instead enter an orbit. The polynomial $x^3-2x+2$ with initial guess $x_0=0$ induces a $2$-orbit, and the polynomial $x^5-x-1$ with initial guess $x_0=0$ induces and $3$-orbit. Given a positive integer $n$ find an example of a polynomial that will induce an $n$-orbit for an initial guess of zero.