-
Determine the value of each limit, if it exists.
\(\displaystyle \lim\limits_{x \to 4} \frac{2x-9}{x+4} \)\(\displaystyle \lim\limits_{x \to -3} \frac{|x+3|}{2x+6} \)\(\displaystyle \lim\limits_{x \to 0.25^{-}} \frac{4x-1}{|4x^3-x^2|} \)\(\displaystyle \lim\limits_{x \to 0^-} \left(\frac{1}{|x|} - \frac{1}{x}\right) \)
-
Determine the value of each limit, or determine that the limit doesn’t exist.
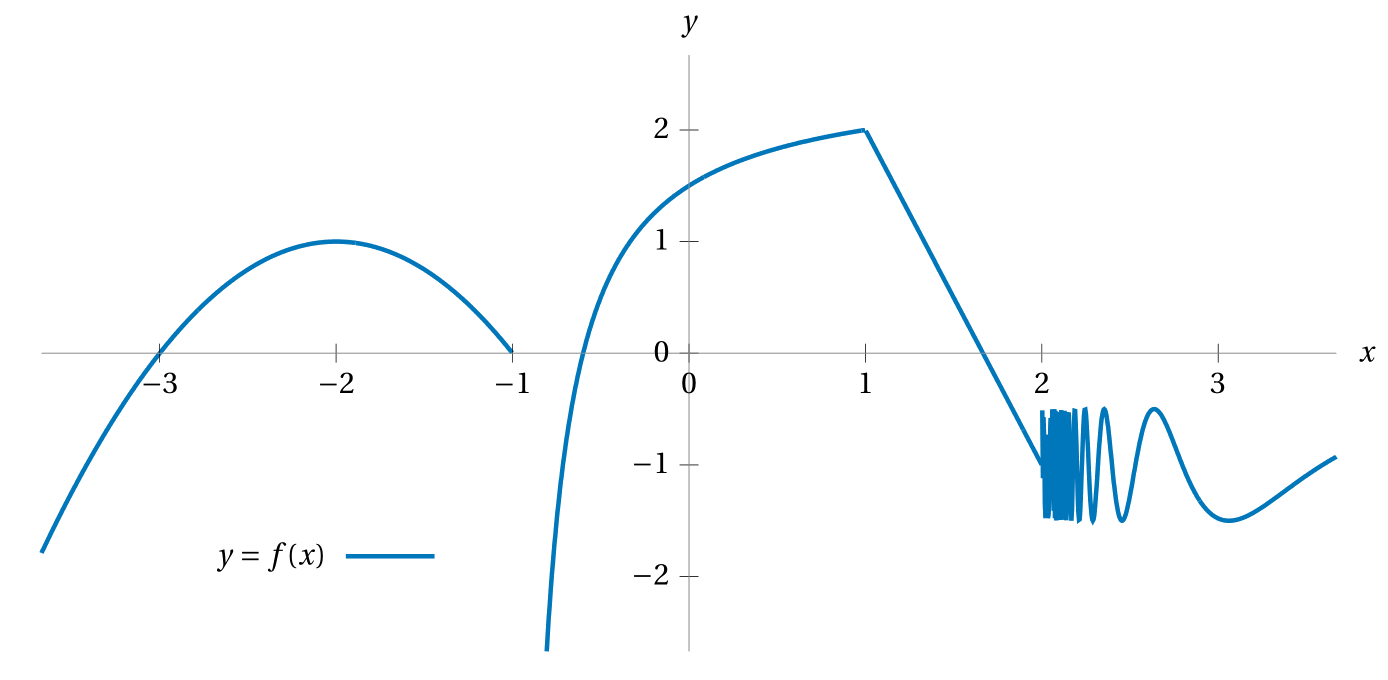\(\displaystyle \lim\limits_{x \to -\infty} f(x) \)\(\displaystyle \lim\limits_{x \to -2} f(x) \)\(\displaystyle \lim\limits_{x \to -1^-} f(x) \)\(\displaystyle \lim\limits_{x \to -1^+} f(x) \)\(\displaystyle \lim\limits_{x \to -1} f(x) \)\(\displaystyle \lim\limits_{x \to 0} f(x) \)\(\displaystyle \lim\limits_{x \to 1^-} f(x) \)\(\displaystyle \lim\limits_{x \to 1^+} f(x) \)\(\displaystyle \lim\limits_{x \to 1} f(x) \)\(\displaystyle \lim\limits_{x \to 2} f(x) \)\(\displaystyle \lim\limits_{x \to \infty} f(x) \) -
Let \(g\) be the function defined piecewise by the following four formulas:
\[
g(x) = \begin{cases}
-x &\text{for } x \lt 1 \qquad &7 &\text{for } x=1
\\x^2-2 &\text{for } 1 \lt x \leq 5 \qquad &7x-5 &\text{for } 5 \lt x
\end{cases}
\]
Evaluate the following. If a limit doesn’t exist, cross it out with confidence.
\( \displaystyle \lim\limits_{x \to 1^-} g(x)\)\( \displaystyle \lim\limits_{x \to 1} g(x)\)\( \displaystyle g(1)\)\( \displaystyle \lim\limits_{x \to 5^-} g(x)\)\( \displaystyle \lim\limits_{x \to 5^+} g(x)\)\( \displaystyle \lim\limits_{x \to 5} g(x)\)
-
Use a computing device to approximate
the value of these limits
accurate to four decimal places.
\(\displaystyle \lim\limits_{x \to \infty} x^{\frac{1}{x}} \)\(\displaystyle \lim\limits_{x \to 0} \; 4\arctan\!\left(x^x\right) \)\(\displaystyle \lim\limits_{x \to \infty} \left(\frac{x}{x+1}\right)^x \)\(\displaystyle \lim\limits_{x \to \infty} \left(1 + \frac{6.65544}{x}\right)^x \)
-
Using the fact that \(\lim_{x \to 0} \sin(x)/x = 1\)
and the “limit laws" demonstrate how to algebraically find
the values of the following limits.
\(\displaystyle \lim\limits_{x \to 0} \frac{\sin(3x)}{7x} \)\(\displaystyle \lim\limits_{x \to 0} \frac{\sin(3x)}{\sin(7x)} \)\(\displaystyle \lim\limits_{x \to 0} \frac{x\cos(x)}{\tan(x)} \)\(\displaystyle \lim\limits_{x \to 0} \frac{\sin^2(2x)}{x^2} \)
-
Without referencing technology,
determine the value of each limit.
\(\displaystyle \lim\limits_{x \to -4} \frac{3x^2+9x-5}{x^2-16} \)\(\displaystyle \lim\limits_{x \to 100} \frac{x-100}{10-\sqrt{x}} \)\(\displaystyle \lim\limits_{x \to 0} \left(\frac{1}{x} - \frac{1}{x^2+1}\right) \)\(\displaystyle \lim\limits_{x \to \infty} \sqrt{x} \)\(\displaystyle \lim\limits_{x \to 7^+} \frac{x^2-x-20}{x-7} \)\(\displaystyle \lim\limits_{x \to 7^+} \frac{x^2-3x-28}{x-7} \)\(\displaystyle \lim\limits_{x \to 7} \frac{49}{(x-7)^2} \)\(\displaystyle \lim\limits_{x \to \infty} \frac{3x^2-7x+5}{2x-1} \)\(\displaystyle \lim\limits_{x \to \infty} \frac{3x^2-7x+5}{(2x-1)^2} \)\(\displaystyle \lim\limits_{x \to \infty} \frac{3x^2-7x+5}{(2x-1)^3} \)\(\displaystyle \lim\limits_{x \to 1} \frac{1-\sqrt{x}}{1-x} \)\(\displaystyle \lim\limits_{x \to 0} \frac{1-\sqrt{1-x^2}}{x} \)\(\displaystyle \lim\limits_{x \to 0} \frac{1-\sqrt{1-x^2}}{x^2} \)
- Let \(g\) be the function defined piecewise in terms of some function \(f\) as follows: \[ g(x) = \begin{cases} -1 &\text{ for } x \lt -3 \\f(x) &\text{ for } -3 \leq x \lt 1 \\-x^2+5 &\text{ for } x \geq 1 \end{cases} \] Find an example of a linear function \(f\) such that \(g\) is continuous. Can you find an example of a non-linear function \(f\) such that \(g\) is continuous? What about a function \(f\) such that \(g\) will have a pole (non-removable discontinuity, asymptote) at \(x=0\) but will be continuous otherwise?
- For functions \(f\) and \(g,\) it may be that \(\lim_{x \to c}\big(f(x) + g(x)\big)\) exists even though neither \(\lim_{x \to c}f(x)\) nor \(\lim_{x \to c}g(x)\) exist. Find examples of such functions.
- For functions \(f\) and \(g,\) it may be that \(\lim_{x \to c}\big(f(x)g(x)\big)\) exists even though neither \(\lim_{x \to c}f(x)\) nor \(\lim_{x \to c}g(x)\) exist. Find examples of such functions.
- How can you very quickly prove that the polynomial \(x^{171}-7x^2-1\) has a root on the domain \([0,2]\) by invoking the Intermediate Value Theorem?
Challenges
-
Patrick Snyder
Demonstrate how to compute the following limit algebraically. \[ \lim_{x\ to 0} \frac{\sqrt{1+\tan(x)}-\sqrt{1+\sin(x)}}{x^3} \] -
James Stewart
Does there exist a number that is exactly one more than its cube?
The challenge is to cunningly answer this question without calculating any such number. - If \(\lim_{x \to c} \big(f(x) + g(x)\big) = 11\) and \(\lim_{x \to c} \big(f(x) - g(x)\big) = 7,\) what must the value of \(\lim_{x \to c} \big(f(x)g(x)\big)\) be?
- Suppose that a function \(f\) defined on some domain \([a,b]\) has the following property: for any \(N\) between \(f(a)\) and \(f(b)\) there exists some \(c\) between \(a\) and \(b\) such that \(f(c) = N.\) Must \(f\) be a continuous function?