Make sure you know how to switch between radian measure and degree measure on your calculator of choice. These exercises are designed in terms of radian measure.
- For what angle \(t\) between \(-\tfrac{\pi}{2}\) and \(\tfrac{\pi}{2}\) does \(\sin(t) = 0.777?\)
- For what angle \(t\) between \(0\) and \(\pi\) does \(\cos(t) = 0.314?\)
- Is there an angle \(t\) such that \(\sin(t) = 2.3?\) If so, what it is? If not, why not?
-
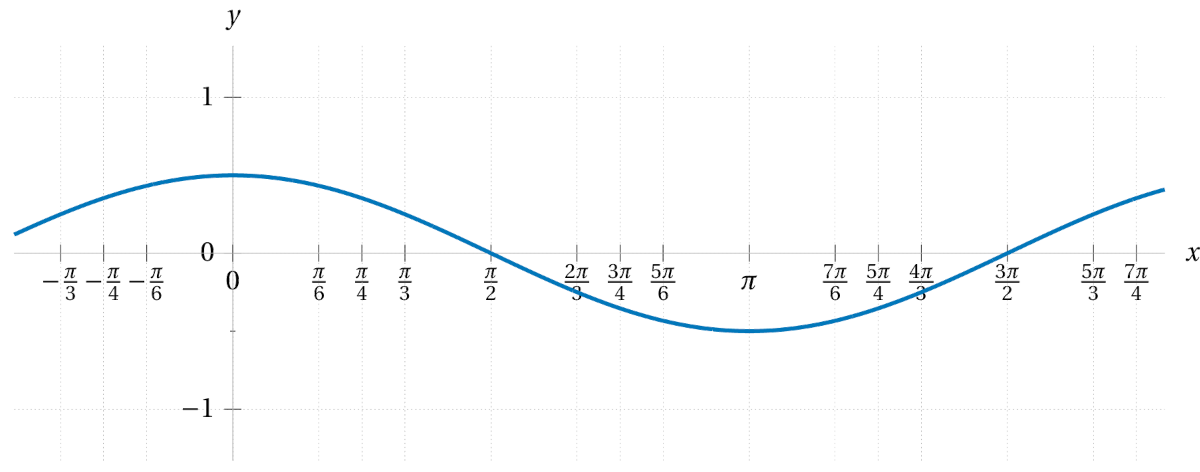
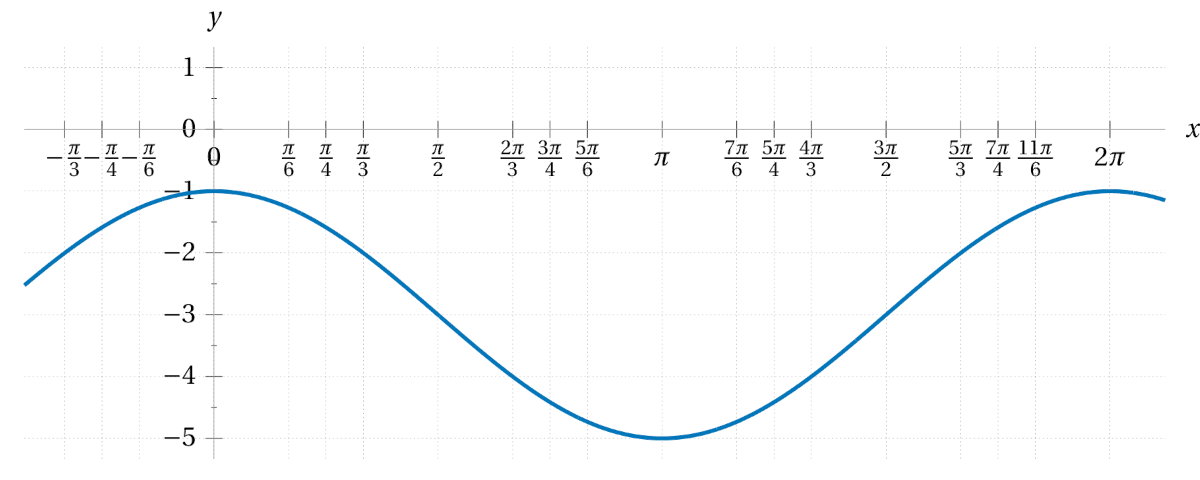
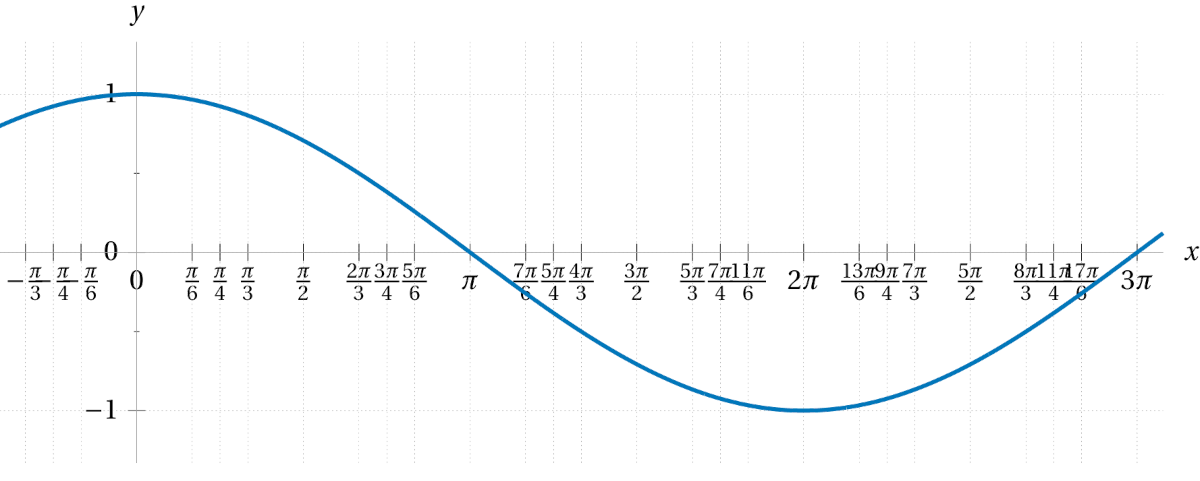
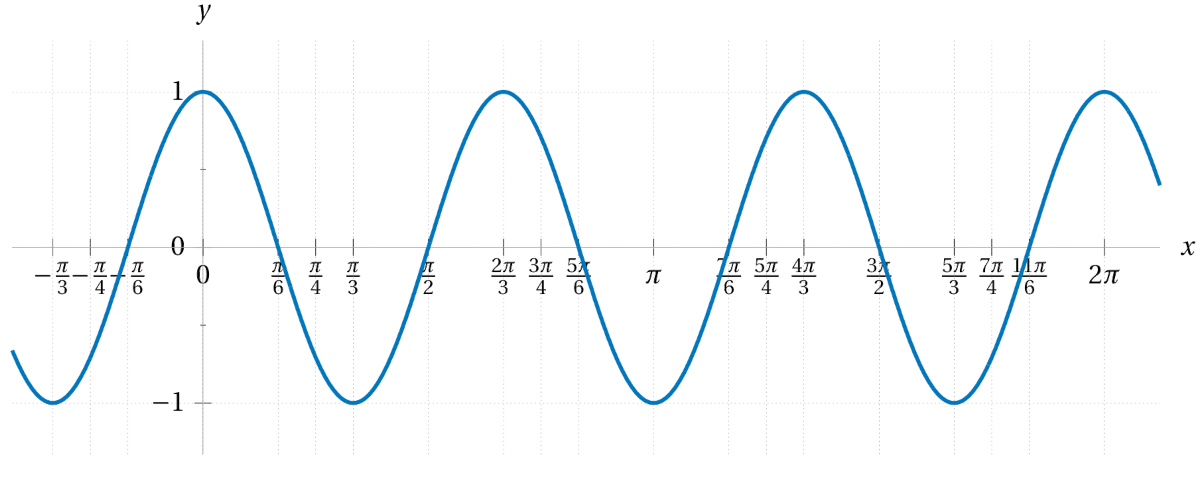
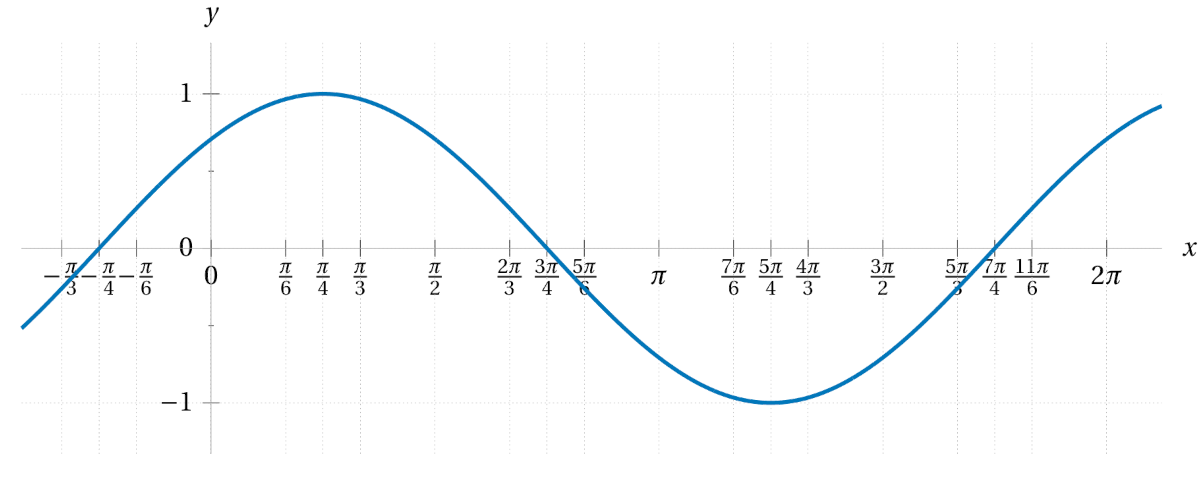
First sketch the graph of \(\sin(x)\) for reference. Then graph each of the following functions, thinking of them as a transformation of the sine function.
\(\displaystyle 2\sin\bigl(x\bigr) \)\(\displaystyle \sin\bigl(2x\bigr) \)\(\displaystyle \sin\bigl(x+2\bigr) \)\(\displaystyle \sin\bigl(x\bigr)+2 \)\(\displaystyle \sin\bigl(x+\tfrac{\pi}{6}\bigr) \)\(\displaystyle \tfrac{1}{3}\sin\bigl(4x\bigr) \)\(\displaystyle 5\sin\bigl(\tfrac{1}{2}x\bigr) \)\(\displaystyle \sin\bigl(x-\tfrac{\pi}{3}\bigr)-1 \)\(\displaystyle \sin\bigl(\tfrac{1}{3}(x+\tfrac{\pi}{4})\bigr) \) - With regards to each of the transformations in the previous exercise, affirm the meaning of the vocabulary terms period, amplitude, and phase shift.
-
Each of the following plots feature the graph of a transformation of the cosine function. First sketch the graph of \(\cos(x)\) for reference. Then write down the formulas for the functions graphed below thinking of them as a transformation of the cosine function.