
 In the plane there are two fundamental ways of describing the location of a point.
After designating an origin point,
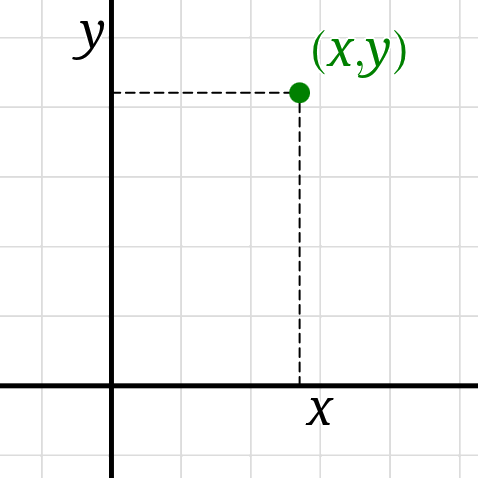
within a rectangular coordinate system a point’s location
is described as a coordinate pair \((x,y)\)
where \(x\) is the point’s eastward distance from the origin
and \(y\) is the point’s northward distance from the origin.
Within a polar coordinate system a point’s location
is described as a coordinate pair \((r,t)\)
where \(r\) is the point’s straight-line distance from the origin
and \(t\) describes the direction of the point relative to the origin,
either as an “angle” \(t\) (measured in radians)
or as an arclength of \(rt\) along the circle on which the point lies.
In the plane there are two fundamental ways of describing the location of a point.
After designating an origin point,
within a rectangular coordinate system a point’s location
is described as a coordinate pair \((x,y)\)
where \(x\) is the point’s eastward distance from the origin
and \(y\) is the point’s northward distance from the origin.
Within a polar coordinate system a point’s location
is described as a coordinate pair \((r,t)\)
where \(r\) is the point’s straight-line distance from the origin
and \(t\) describes the direction of the point relative to the origin,
either as an “angle” \(t\) (measured in radians)
or as an arclength of \(rt\) along the circle on which the point lies.
The sine and cosine functions,
along with the arctangent (tan⁻¹) function,
are simply the means by which we convert between these two coordinate systems.
The study of trigonometry is an extended commentary
on the geometry of these conversions.
\[
\begin{align*}
x&=r\cos(t)
\\ y&=r\sin(t)
\end{align*}
\quad
\longleftrightarrow
\quad
\begin{align*}
r&=\sqrt{x^2+y^2}
\\ t&=\operatorname{arctan}\bigl(\tfrac{y}{x}\bigr)
\end{align*}
\]