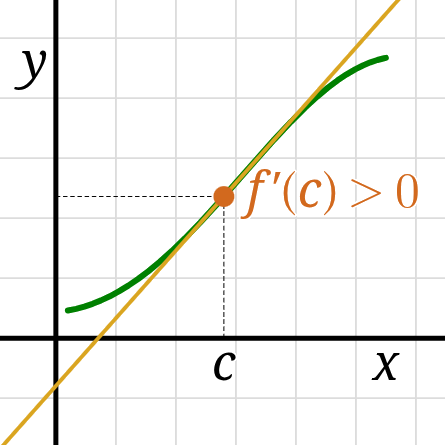
 A continuous function \(f\) is increasing on an interval
if for every two numbers \(a\) and \(b\) in that interval
for which \(a \lt b\) we have \(f(a) \lt f(b).\)
Since the derivative \(f'(c)\) is the rate at which \(f\) is changing at \(x=c,\)
we can also conclude that \(f\) is increasing on an interval
if \(f'(c) \gt 0\) for all \(c\) in that interval.
Similarly a function \(f\) is decreasing on an interval
if for every two numbers \(a\) and \(b\) in that interval
for which \(a \lt b\) we have \(f(a) \gt f(b),\)
or \(f'(c) \lt 0\) for all \(c\) in that interval.
I.e. positive slope corresponds to a function increasing
and a negative slope correspond to a function decreasing.
A continuous function \(f\) is increasing on an interval
if for every two numbers \(a\) and \(b\) in that interval
for which \(a \lt b\) we have \(f(a) \lt f(b).\)
Since the derivative \(f'(c)\) is the rate at which \(f\) is changing at \(x=c,\)
we can also conclude that \(f\) is increasing on an interval
if \(f'(c) \gt 0\) for all \(c\) in that interval.
Similarly a function \(f\) is decreasing on an interval
if for every two numbers \(a\) and \(b\) in that interval
for which \(a \lt b\) we have \(f(a) \gt f(b),\)
or \(f'(c) \lt 0\) for all \(c\) in that interval.
I.e. positive slope corresponds to a function increasing
and a negative slope correspond to a function decreasing.
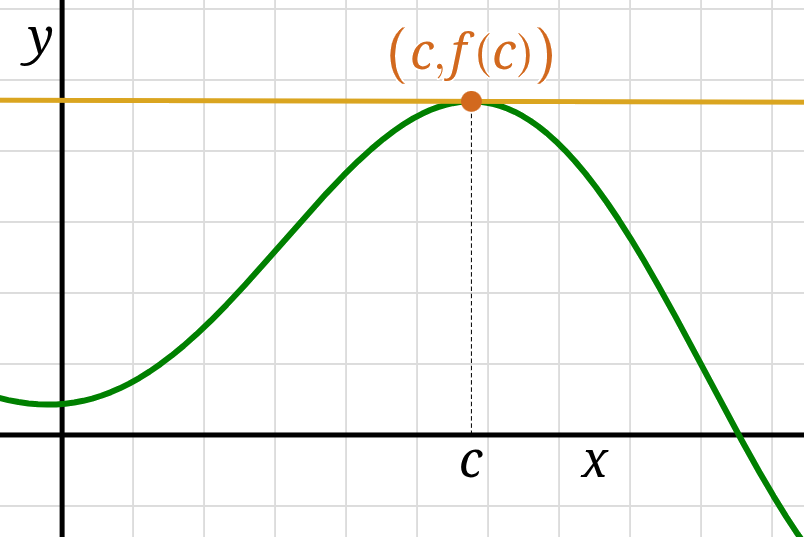 A function \(f\) has a relative (local) minimum at \(x = c\)
if \(f(c) \lt f(x)\) for all \(x\) around \(c;\)
the number \(f(c)\) is the relative minimum value.
Similarly a function \(f\) has a relative (local) maximum at \(x = c\)
if \(f(c) \gt f(x)\) for all \(x\) around \(c;\)
the number \(f(c)\) is the relative maximum value.
A relative minimum or maximum is generally referred to
as a relative (local) extremum (pl. extrema),
and the point \(\bigl(c, f(c)\bigr)\) is called an extreme point.
Sometimes these are also referred to as “turning points”.
Fact: if \(f(c)\) is a relative extremum of \(f\),
then either \(f'(c) = 0\) or \(f'(c)\) doesn’t exist.
Due to this fact, every value \(c\) at which
either \(f'(c) = 0\) or \(f'(c)\) doesn’t exist
is a candidate to be a relative extremum of \(f.\)
Such candidate values are typically referred to
as critical values of \(f.\)
A critical value \(c\) will sincerely correspond to an extremum of \(f\)
if \(f'\) changes sign (\(\pm\)) on either side of \(c:\)
if \(f'(x) \lt 0\) for \(x \lt c\) and \(f'(x) \gt 0\) for \(x \gt c\)
then \(f\) has a relative minimum at \(x = c,\)
and similarly if \(f'(x) \gt 0\) for \(x \lt c\) and \(f'(x) \lt 0\) for \(x \gt c\)
then \(f\) has a relative maximum at \(x = c.\)
This analysis is typically referred to as the
first-derivative test.
A function \(f\) has a relative (local) minimum at \(x = c\)
if \(f(c) \lt f(x)\) for all \(x\) around \(c;\)
the number \(f(c)\) is the relative minimum value.
Similarly a function \(f\) has a relative (local) maximum at \(x = c\)
if \(f(c) \gt f(x)\) for all \(x\) around \(c;\)
the number \(f(c)\) is the relative maximum value.
A relative minimum or maximum is generally referred to
as a relative (local) extremum (pl. extrema),
and the point \(\bigl(c, f(c)\bigr)\) is called an extreme point.
Sometimes these are also referred to as “turning points”.
Fact: if \(f(c)\) is a relative extremum of \(f\),
then either \(f'(c) = 0\) or \(f'(c)\) doesn’t exist.
Due to this fact, every value \(c\) at which
either \(f'(c) = 0\) or \(f'(c)\) doesn’t exist
is a candidate to be a relative extremum of \(f.\)
Such candidate values are typically referred to
as critical values of \(f.\)
A critical value \(c\) will sincerely correspond to an extremum of \(f\)
if \(f'\) changes sign (\(\pm\)) on either side of \(c:\)
if \(f'(x) \lt 0\) for \(x \lt c\) and \(f'(x) \gt 0\) for \(x \gt c\)
then \(f\) has a relative minimum at \(x = c,\)
and similarly if \(f'(x) \gt 0\) for \(x \lt c\) and \(f'(x) \lt 0\) for \(x \gt c\)
then \(f\) has a relative maximum at \(x = c.\)
This analysis is typically referred to as the
first-derivative test.