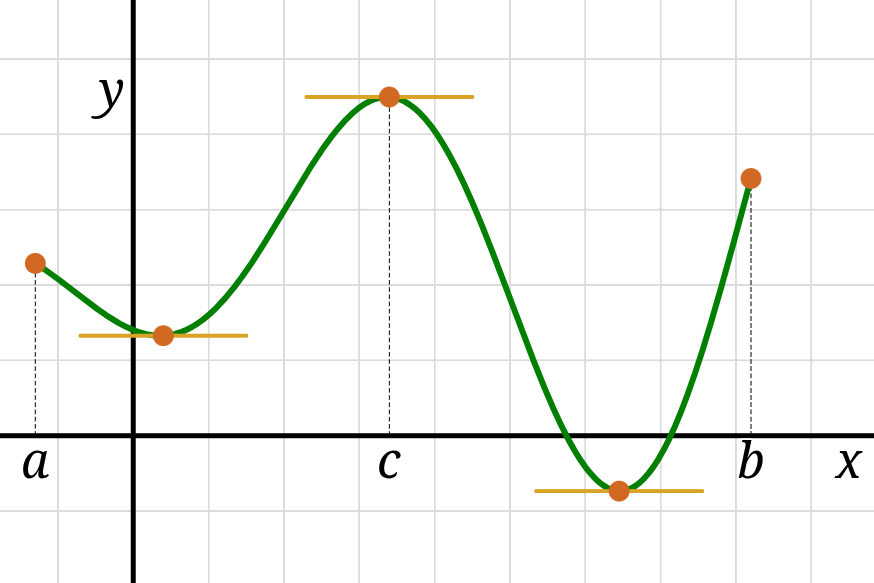
A function \(f\) has an absolute (global) minimum at \(x = c\)
if \(f(c) \lt f(x)\) for all \(x\) in the domain of \(f;\)
the number \(f(c)\) is the absolute minimum value.
Similarly a function \(f\) has a absolute (global) maximum at \(x =c\)
if \(f(c) \gt f(x)\) for all \(x\) in the domain of \(f;\)
the number \(f(c)\) is the absolute maximum value.
An absolute minimum or maximum is generally referred to
as an absolute (global) extremum (pl. extrema).
In general a continuous function may not have global extrema,
but if it does the extrema must occur at a critical value
— a value \(c\) for which \(f'(c) = 0\) or \(f'(c)\) doesn’t exist —
or at a point on the boundary of the function’s domain.
Extreme value theorem:
“If \(f\) is continuous on a closed interval \([a,b]\)
then it must have an absolute minimum
and an absolute maximum on that interval.”
Procedure for finding extreme values of a function \(f\) defined on a closed interval \([a,b]:\)
- Determine all possible values of \(c\) in the domain of \(f\) for which \(f'(c) = 0\) or \(f'(c)\) is not defined.
- Calculate \(f(c)\) for each of those values of \(c,\) and calculate \(f(a)\) and \(f(b).\) Among all of those output values, the largest will be the absolute maximum and the smallest will be the absolute minimum.