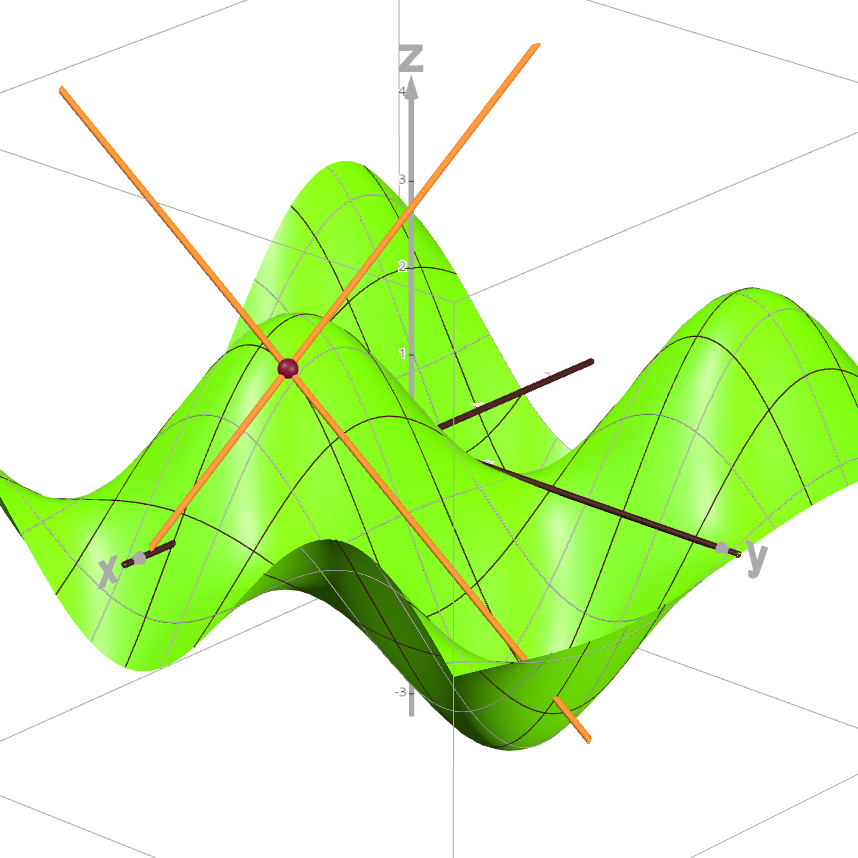
Functions are not limited to taking only a single independent variable as input. We refer to a function of more than one independent variable as a multivariable function. For example, \(f(x,y)\) is the formula for a 2-variable function, and letting \(z = f(x,y)\) we can consider the graph of \(f,\) a surface, in three dimensional \(xyz\)-space. For such a multivariable function \(f\) with formula \(f(x,y)\) its partial derivatives with respect to \(x\) and \(y\) are defined and denoted as:
 The \(\partial\) symbol is pronounced
The \(\partial\) symbol is pronounced partial
.
These are only partial derivatives because the full derivative
of a multivariable function is not just a single function, but a matrix of functions.
These partial derivatives represent the rates-of-change of \(f\)
in the \(x\)- and \(y\)-direction or, geometrically,
the slopes of the lines tangent to the graph of \(f\) in those directions.
To determine formulas for these partial derivatives from a formula for \(f,\)
all the rules of single-variable differentiation can be applied
while pretending the other variable is just a constant.
The second-order partial derivatives of \(f,\)
the results of differentiating \(f\) twice
with respect to some order of \(x\) and \(y,\)
are denoted as:
\[
\displaystyle f_{xx} = \frac{\partial^2 f}{\partial x^2}
\qquad\quad
\displaystyle f_{xy} = \frac{\partial^2 f}{\partial y\partial x}
\qquad\quad
\displaystyle f_{yx} = \frac{\partial^2 f}{\partial x\partial y}
\qquad\quad
\displaystyle f_{yy} = \frac{\partial^2 f}{\partial y^2}
\]