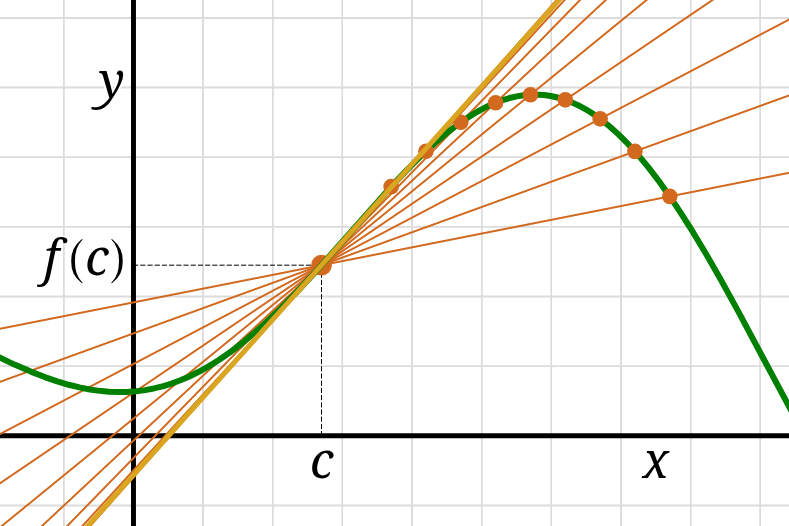
 The instantaneous rate-of-change of a continuous function \(f\)
at \(x=c\) is \[ \lim\limits_{h\to 0}\frac{f(c+h)-f(c)}{h}\,. \]
On the graph of \(f\) this is the slope of the line
that just barely touches point \(\bigl(c, f(c)\bigr)\)
referred to as the tangent line at this point.
Similarly we say that the line is tangent to the graph at \(x=c\)
and call \(\bigl(c, f(c)\bigr)\) the point of tangency.
This slope and the instantaneous rate-of-change of \(f\)
can only be defined if \(f\) is continuous around \(c,\) if that limit exists.
When this limits exists, we say \(f\) is differentiable at \(x=c.\)
The instantaneous rate-of-change of a continuous function \(f\)
at \(x=c\) is \[ \lim\limits_{h\to 0}\frac{f(c+h)-f(c)}{h}\,. \]
On the graph of \(f\) this is the slope of the line
that just barely touches point \(\bigl(c, f(c)\bigr)\)
referred to as the tangent line at this point.
Similarly we say that the line is tangent to the graph at \(x=c\)
and call \(\bigl(c, f(c)\bigr)\) the point of tangency.
This slope and the instantaneous rate-of-change of \(f\)
can only be defined if \(f\) is continuous around \(c,\) if that limit exists.
When this limits exists, we say \(f\) is differentiable at \(x=c.\)
Big idea: rather than describing the instantaneous rate-of-change of \(f\) at a specific point \(x=c,\) we can keep \(x\) generic and define the function that describes the instantaneous rate-of-change of \(f\) at any point. The derivative of \(f\) with respect to \(x,\) denoted either as \(f'\) (which we read as “\(f\) prime”) or as \(\frac{\mathrm{d}f}{\mathrm{d}x},\) is \[ f'(x) = \lim\limits_{h \to 0}\frac{f(x+h)-f(x)}{h}\,. \] The \(\frac{\mathrm{d}f}{\mathrm{d}x}\) notation alludes to the derivative being a slope; the \(\mathrm{d}\) in that notation may be read as “a small deviation in,” and so \(\frac{\mathrm{d}f}{\mathrm{d}x}\) may be read as “a small deviation in the output per a small deviation in the input.”