A region is unbounded if there is no upper limit on the distance between any two points within the region. An unbounded region, though it stretches off towards infinity, may still contain a definite, finite, measurable area. An improper integral is a definite integral that describes an unbounded region. An improper integral can be evaluated by taking a limit as the integral’s bound approaches the unbounded portion of the region. If that limit exists we say the improper integral converges but if it doesn’t exist we say the improper integral diverges.
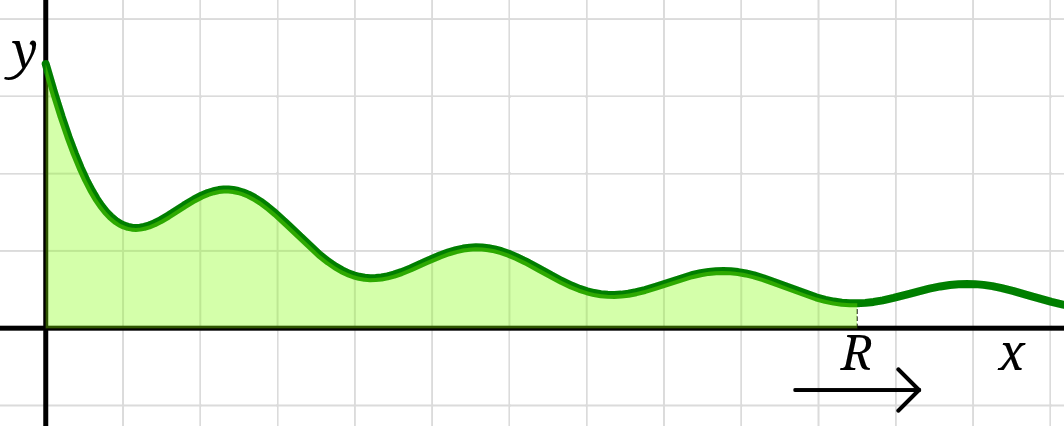One possibility is a region being unbounded in the left-right direction,
the \(x\)-axis being an asymptote of the graph that defines the upper bound of the region,
and a bound of the integral being \(+\infty\) or \(-\infty,\)
in which case the area of the region is:
\[
\int\limits_0^\infty f(x) \,\mathrm{d}x
= \lim\limits_{R \to \infty}\int\limits_0^R f(x) \,\mathrm{d}x
\]
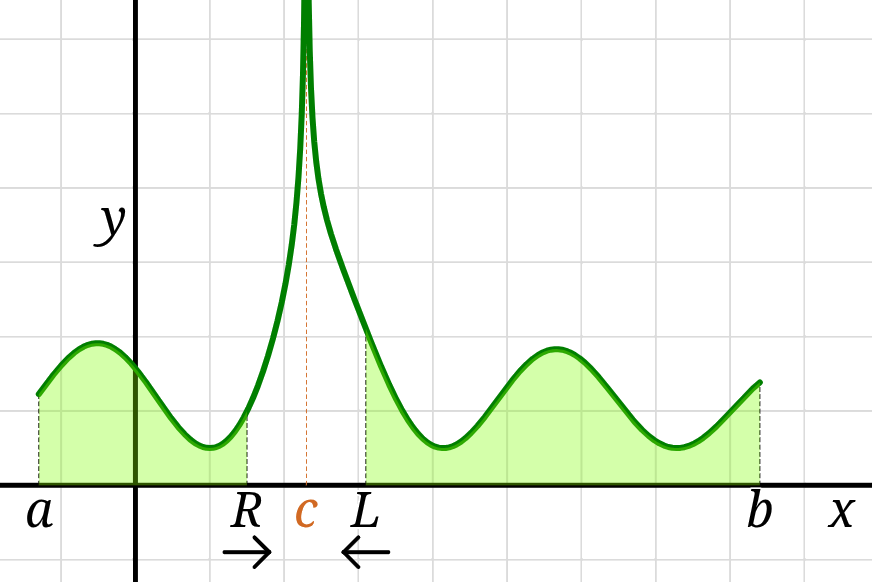Another possibility is that the function has a pole,
a discontinuity corresponding to a vertical asymptote of the graph
between the bounds of integration,
in which case the integral must be split up into two integrals,
one on either side of the discontinuity.
The area of such a region is:
\[
\int\limits_a^b f(x) \,\mathrm{d}x
= \lim\limits_{R \to c^-}\int\limits_a^R f(x) \,\mathrm{d}x
+ \lim\limits_{L \to c^+}\int\limits_L^b f(x) \,\mathrm{d}x
\]