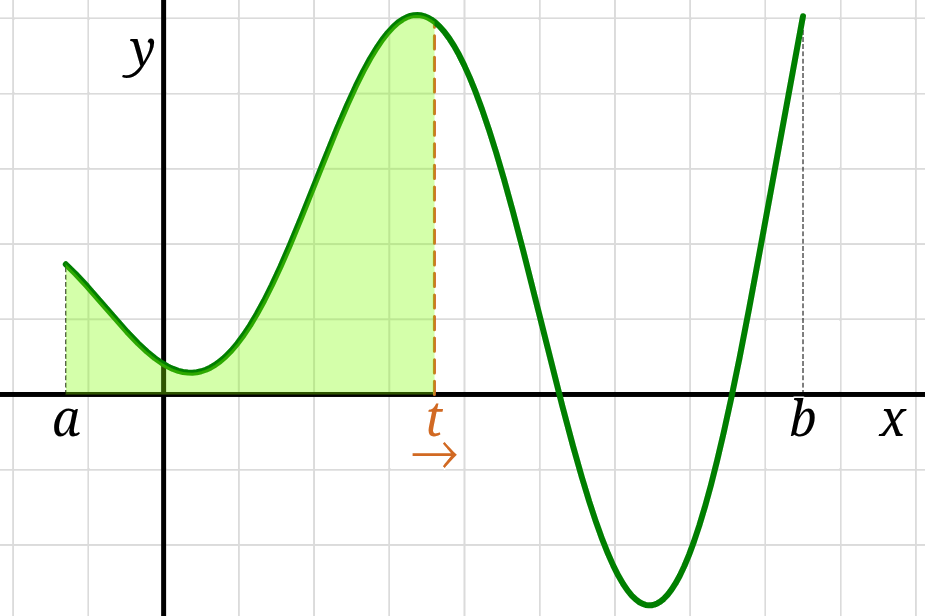
 The FTC, Part I –
For a function \(f\) that is continuous on the interval \([a,b],\) we have
\[ \frac{\mathrm{d}}{\mathrm{d}t} \int\limits_a^t f(x) \,\mathrm{d}x = f(t) \,.\]
In a sense, differentiation and integration are “inverse” operations.
The operation of differentiation \(\frac{\mathrm{d}}{\mathrm{d}t}\)
“undoes” the operation of integration
when we are differentiating with respect to the upper bound of the integral.
The FTC, Part I –
For a function \(f\) that is continuous on the interval \([a,b],\) we have
\[ \frac{\mathrm{d}}{\mathrm{d}t} \int\limits_a^t f(x) \,\mathrm{d}x = f(t) \,.\]
In a sense, differentiation and integration are “inverse” operations.
The operation of differentiation \(\frac{\mathrm{d}}{\mathrm{d}t}\)
“undoes” the operation of integration
when we are differentiating with respect to the upper bound of the integral.
The FTC, Part II – For a function \(f\) that is continuous on the interval \([a,b]\) for which \(F\) is any antiderivative of \(f,\) we have \[ \int\limits_a^b f(x) \,\mathrm{d}x = F(b)-F(a)\,. \] A definite integral can be computed as a difference of antiderivatives of the integrand evaluated at the bounds of the integral. I.e. the area of the region under the graph of a function can be computed exactly, without referring to geometry or numerical approximations, so long as an antiderivative of the function can be determined.