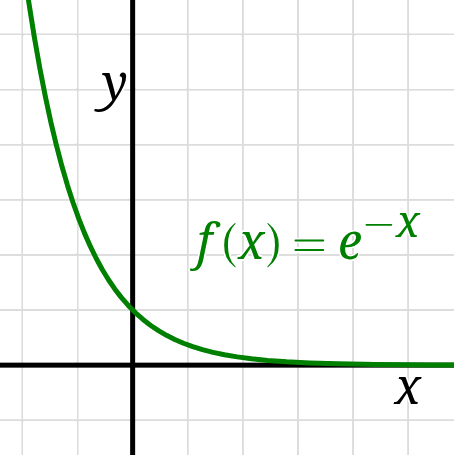
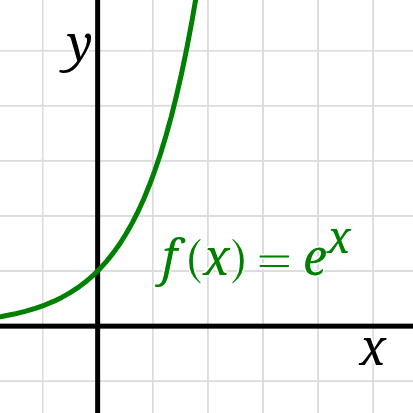
 An exponential function’s output
changes at a rate proportional to its current value.
The exponential function of base-\(b\) has formula \(f(x) = b^x.\)
The function is “growing” for \(b \gt 1\) and “decaying” for \(0 \lt b \lt 1.\)
Exponential functions are often instead expressed in the “natural” form
\(f(x) = \mathrm{e}^{kx}\) for constant \(\mathrm{e} \approx 2.71\) and parameter \(k,\)
where now \(k \gt 0\) corresponds to growth and \(k \lt 0\) corresponds to decay.
An exponential function’s output
changes at a rate proportional to its current value.
The exponential function of base-\(b\) has formula \(f(x) = b^x.\)
The function is “growing” for \(b \gt 1\) and “decaying” for \(0 \lt b \lt 1.\)
Exponential functions are often instead expressed in the “natural” form
\(f(x) = \mathrm{e}^{kx}\) for constant \(\mathrm{e} \approx 2.71\) and parameter \(k,\)
where now \(k \gt 0\) corresponds to growth and \(k \lt 0\) corresponds to decay.
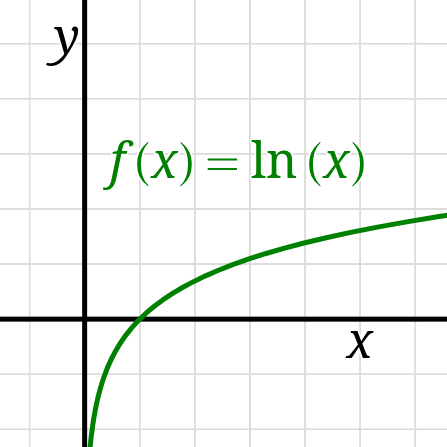 Logarithmic functions are the inverses of exponential functions:
the base-\(b\) logarithmic function with formula \(\log_b(x)\)
is the inverse of the exponential function with formula \(b^x.\)
Algebraically, \(y = b^x\) means the same thing as \(\log_b(y) = x.\)
There are “rules” of logarithms analogous to the “rules” of exponentiation:
\[
\log_b(1) = 0
\qquad\qquad
\log_b(xy) = \log_b(x) + \log_b(y)
\qquad\qquad
\log_b\bigl(x^y\bigr) = y\log_b(x)
\]
\[
\frac{\log_b(x)}{\log_b(y)} = \log_y(x)
\qquad\qquad
\log_b\bigl(\tfrac{x}{y}\bigr) = \log_b(x) - \log_b(y)
\qquad\qquad
\log_b\bigl(\sqrt[y]{x}\bigr) = \tfrac{1}{y}\log_b(x)
\]
The “default” base for a logarithm is ten;
a logarithm written as \(\log(x)\) with no base specified is implied to be base-10.
The “natural” base for a logarithm is \(\mathrm{e} \approx 2.71,\)
which garners it’s own dedicated notation, \(\ln(x).\)
The number \(\mathrm{e},\) sometimes referred to as Euler’s number,
is a transcendental numbers, and its decimal representation has no regular pattern.
Logarithmic functions are the inverses of exponential functions:
the base-\(b\) logarithmic function with formula \(\log_b(x)\)
is the inverse of the exponential function with formula \(b^x.\)
Algebraically, \(y = b^x\) means the same thing as \(\log_b(y) = x.\)
There are “rules” of logarithms analogous to the “rules” of exponentiation:
\[
\log_b(1) = 0
\qquad\qquad
\log_b(xy) = \log_b(x) + \log_b(y)
\qquad\qquad
\log_b\bigl(x^y\bigr) = y\log_b(x)
\]
\[
\frac{\log_b(x)}{\log_b(y)} = \log_y(x)
\qquad\qquad
\log_b\bigl(\tfrac{x}{y}\bigr) = \log_b(x) - \log_b(y)
\qquad\qquad
\log_b\bigl(\sqrt[y]{x}\bigr) = \tfrac{1}{y}\log_b(x)
\]
The “default” base for a logarithm is ten;
a logarithm written as \(\log(x)\) with no base specified is implied to be base-10.
The “natural” base for a logarithm is \(\mathrm{e} \approx 2.71,\)
which garners it’s own dedicated notation, \(\ln(x).\)
The number \(\mathrm{e},\) sometimes referred to as Euler’s number,
is a transcendental numbers, and its decimal representation has no regular pattern.
\({\mathrm{e} \approx 2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427427466391932003059921817413596629043572900334295260595630738132328627943490763233829880753195251019011573834187930702154089149934884167509244761460668082264800168477411853742345442437107539077744992069551702761838606261331384583000752044933826560297606737113200709328709127443747047230696977209310141692836819025515108657463772111252389784425056953696770785449969967946864454905987931636889230098793127736178215424999229576351482208269895193668033182528869398496465105820939239829488793320362509443117301238197068416140397019837679320683282376464804295311802328782509819455815301756717361332069811250996181881593041690351598888519345807273866738589422879228499892086805825749279610484198444363463244968487560233624827041978623209002160990235304369941849146314093431738143640546253152096183690888707016768396424378140592714563549061303107208510383750510115747704171898610687396965521267154688957035035402123407849819334321068170121005627880235193033224745015853904730419957777093503660416997329725088687696640355570716226844716256079882651787134195124665201030592123667719432527867539855894489697096409754591856956380236370162112047742722836489613422516445078182442352948636372141740238893441247963574370263755294448337998016125492278509257782562092622648326277933386566481627725164019105900491644998289315056604725802778631864155195653244258698294695930801915298721172556347546396447910145904090586298496791287406870504895858671747985466775757320568128845920541334053922000113786300945560688166740016984205580403363795376452030402432256613527836951177883863874439662532249850654995886234281899707733276171783928034946501434558897071942586398772754710962953741521115136835062752602326484728703920764310059584116612054529703023647254929666938115137322753645098889031360205724817658511806303644281231496550704751025446501172721155519486685080036853228183152196003735625279449515828418829478761085263981395599006737648292244375287184624578036192981971399147564488262603903381441823262515097482798777996437308997038886778227138360577297882412561190717663946507063304527954661855096666185664709711344474016070462621568071748187784437143698821855967095910259686200235371858874856965220005031173439207321139080329363447972735595527734907178379342163701205005451326383544000186323991490705479778056697853358048966906295119432473099587655236812859041383241160722602998330535370876138939639177957454016137223618789365260538155841587186925538606164779834025435128439612946035291332594279490433729908573158029095863138268329147711639633709240031689458636060645845925126994655724839186564209752685082307544254599376917041977780085362.}\)