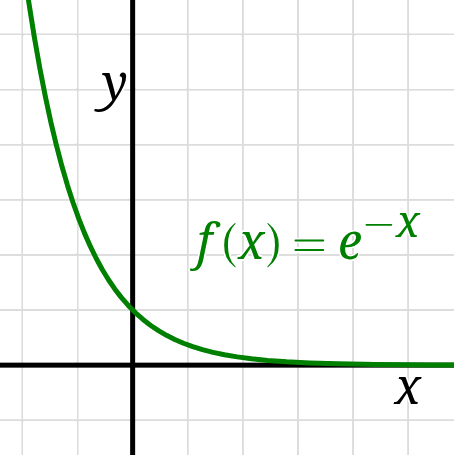
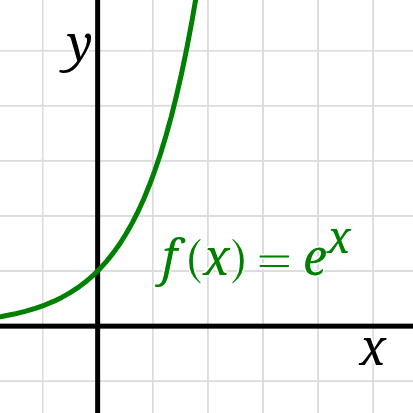
An exponential function’s output
changes at a rate proportional to its current value,
exhibiting unlimited growth.
The exponential function \(P(t) = \mathrm{e}^{kt}\)
is the only function that satisfies the differential equation
\(\frac{\mathrm{d}P}{\mathrm{d}t} = k P.\)
The parameter \(k\) is the exponential rate;
for \(k \gt 0\) its called the growth rate
and for \(k \lt 0\) its called the decay rate.
For positive \(k\) (growth) exponential functions
are often used to model growing populations or appreciating financial values.
For negative \(k\) (decay) exponential functions
are often used to model radioactive decay or depreciating financial values.
Note that \(k\) will be an instantaneous rate-of-change,
and will be different from the rate-of-change over some fixed duration.
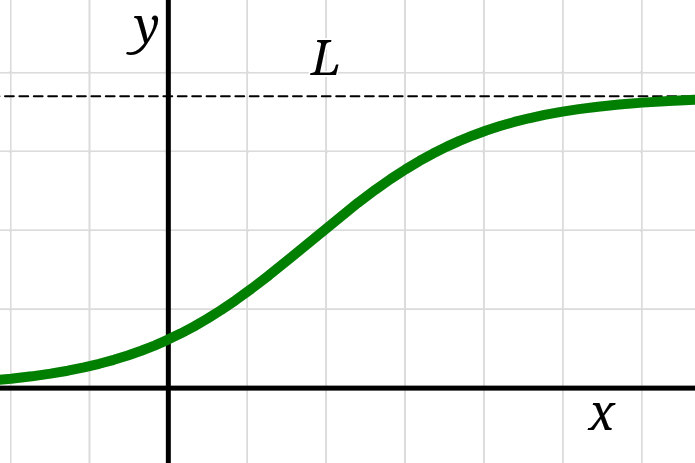A logistic function’s output
changes at a rate proportional to the product of its current value
and its value’s distance to some upper-limit \(L,\)
exhibiting limited growth.
The logistic function \[{P(t) = \frac{L}{1+C\mathrm{e}^{-Lkt}}}\]
is the only function that satisfies the differential equation
\({\frac{\mathrm{d}P}{\mathrm{d}t} = k\bigl(P\bigr)\bigl(L-P\bigr)}.\)
The parameter \(k\) is the logistic rate,
and \(L\) is the upper-limit on the value of \(P\),
often referred to as the carrying capacity
when the logistic function is modelling a population.