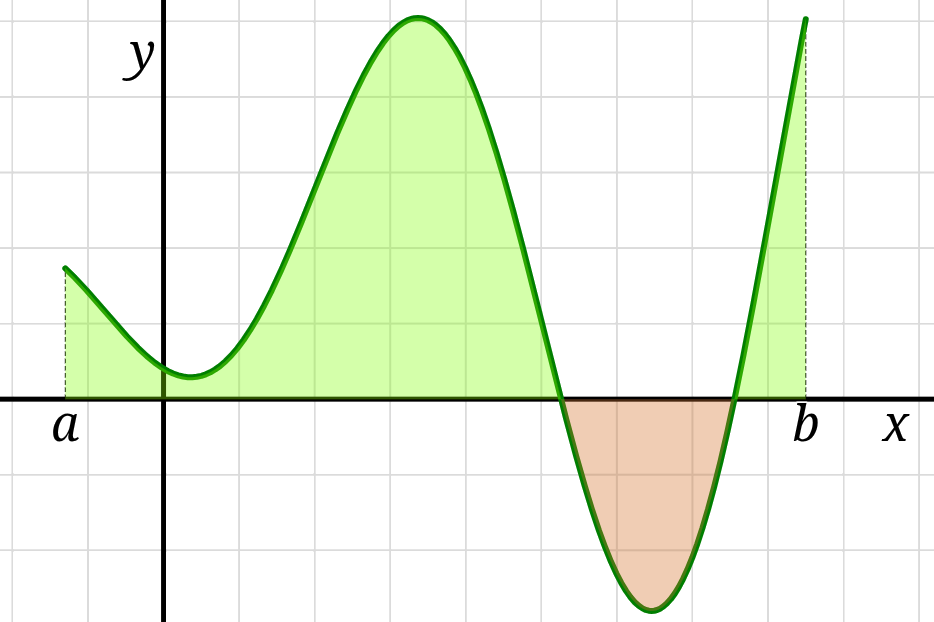
For a function \(f\) defined on \((a,b),\)
the definite integral of \(f\) from \(a\) to \(b,\)
denoted \[ \int_a^b f(x) \,\mathrm{d}x\,, \]
represents the signed area of the region bounded between
the graph of \(f\) and the \(x\)-axis and the vertical lines \(x=a\) and \(x=b.\)
We refer to \(f\) as the integrand
and to \(a\) and \(b\) as the lower bound and upper bound of the integral respectively.
The definite integral counts the amount of area that \(f\) accumulates
as \(x\) sweeps from \(a\) to \(b.\)
Any portion of the region underneath the \(x\)-axis
counts negatively towards the accumulated area.
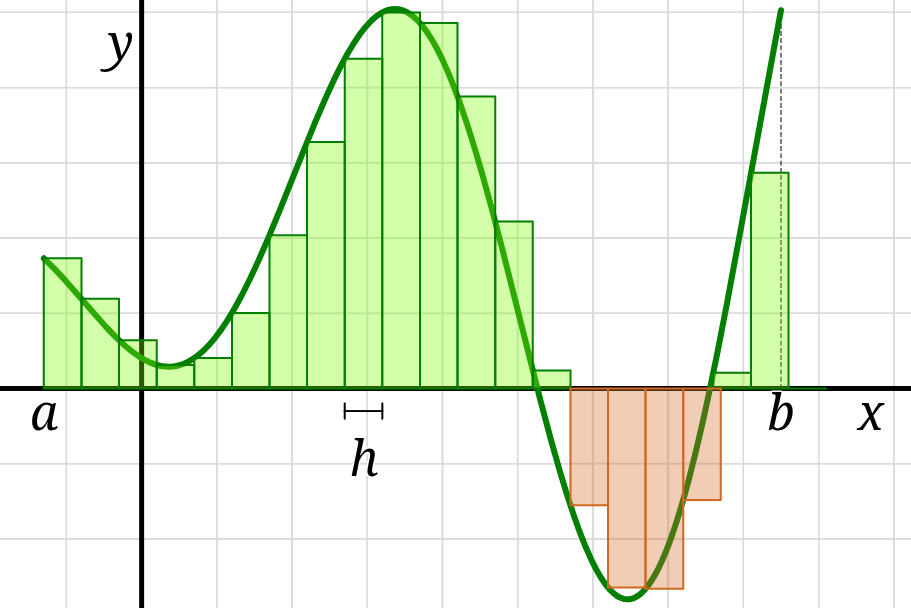A Riemann sum is a sum of the areas of a collection of rectangles,
each of the same uniform width and with a height determined by the function’s graph,
that approximates the area \(\int_a^b f(x)\,\mathrm{d}x.\)
For \(n\) rectangles, each rectangle’s width will be \(h = \frac{b-a}{n}.\)
As \(n\) increases, the value of the sum approaches the area of the region.
For large values of \(n\) this sum becomes unwieldy to write though,
so we invent a new notation, sigma summation notation.
\[ \sum_{i=1}^{n} h \times f(a+ih) \]
is read as “the sum of the areas \(h \times f(a+ih)\) starting at \(i=1\) and counting up to \(i=n\).”