Whereas the sign (\(\pm\)) of \(f'\) dictates whether the function is increasing or decreasing, the sign of \(f''\) dictates whether the function is accelerating or decelerating, whether the graph is concave up or concave down. The graph of \(f\) is concave up on any interval for which \(f''(x) \gt 0\) and the graph of \(f\) is concave down on any interval for which \(f''(x) \lt 0.\)
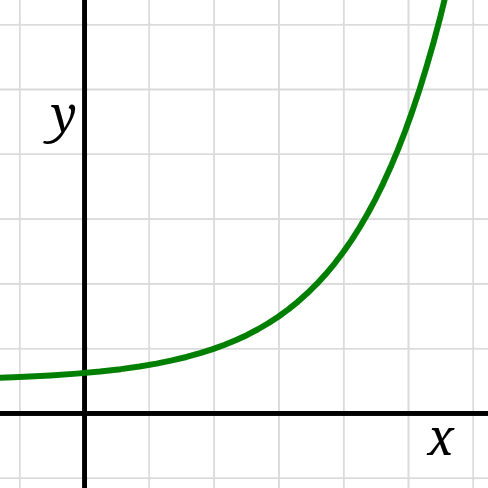
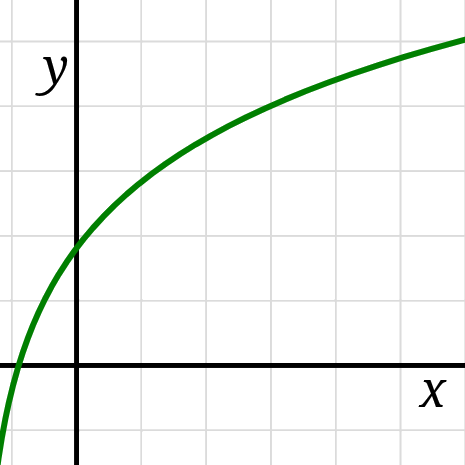
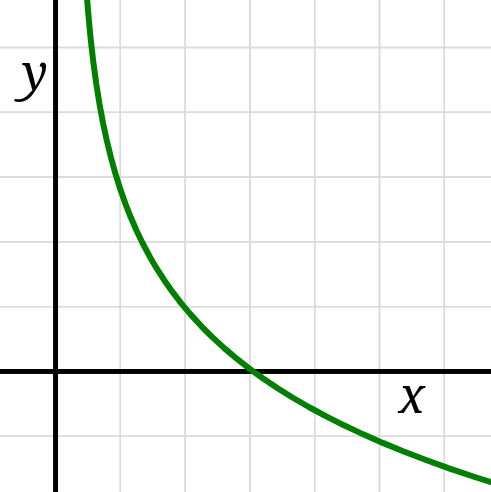
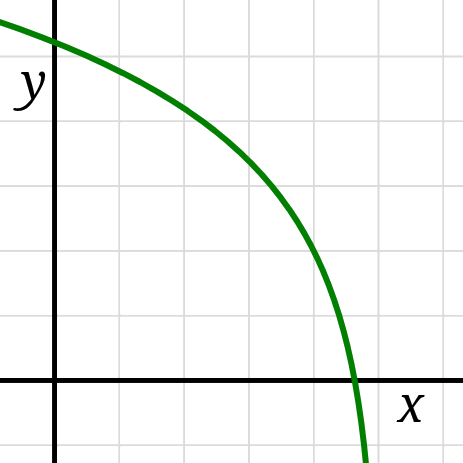
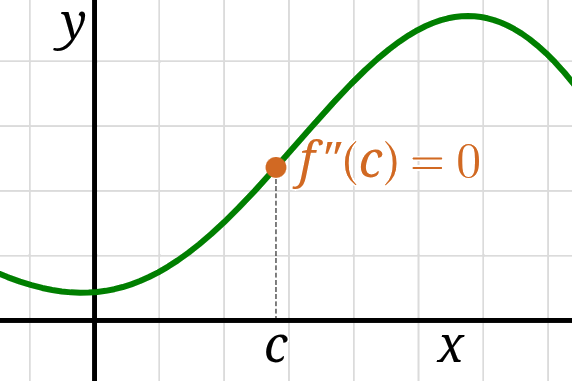 If a function \(f\) has an inflection point at \(x=c,\)
a point where the graph is neither concave up or down
and where it’s potentially switching concavity,
then either \(f''(c) = 0\) or \(f''\) isn’t defined at \(c.\)
Supposing \(f\) has a local extremum at \(x=c,\)
if \(f''(c) \gt 0\) then the extremum must be a local minimum,
and if \(f''(c) \lt 0\) then the extremum must be a local maximum.
This analysis is typically referred to as the
second-derivative test.
If a function \(f\) has an inflection point at \(x=c,\)
a point where the graph is neither concave up or down
and where it’s potentially switching concavity,
then either \(f''(c) = 0\) or \(f''\) isn’t defined at \(c.\)
Supposing \(f\) has a local extremum at \(x=c,\)
if \(f''(c) \gt 0\) then the extremum must be a local minimum,
and if \(f''(c) \lt 0\) then the extremum must be a local maximum.
This analysis is typically referred to as the
second-derivative test.