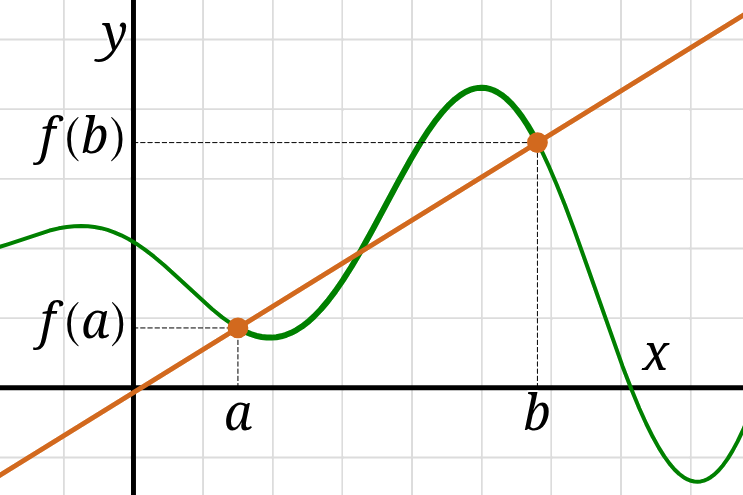
 The average rate-of-change of a continuous function \(f\)
between \(x=a\) and \(x=b\) is \[ \frac{f(b)-f(a)}{b-a}\,. \]
We also call it the average rate-of-change on the interval \([a,b].\)
On the graph of \(f\) this is the slope of the line that passes through
the points \(\bigl(a, f(a)\bigr)\) and \(\bigl(b, f(b)\bigr),\)
referred to as the secant line through these points.
The slope of this secand line and the average rate-of-change of \(f\)
are only equal if \(f\) is continuous between \(a\) and \(b.\)
The average rate-of-change of a continuous function \(f\)
between \(x=a\) and \(x=b\) is \[ \frac{f(b)-f(a)}{b-a}\,. \]
We also call it the average rate-of-change on the interval \([a,b].\)
On the graph of \(f\) this is the slope of the line that passes through
the points \(\bigl(a, f(a)\bigr)\) and \(\bigl(b, f(b)\bigr),\)
referred to as the secant line through these points.
The slope of this secand line and the average rate-of-change of \(f\)
are only equal if \(f\) is continuous between \(a\) and \(b.\)
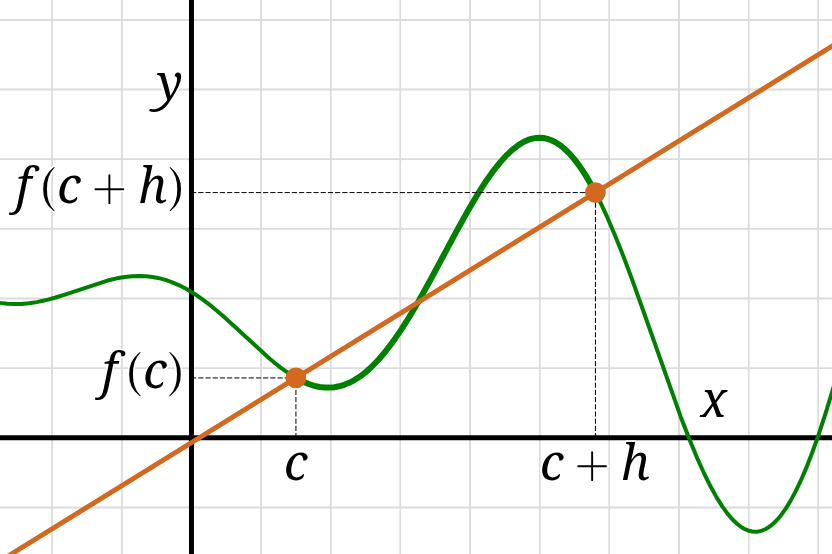 Same idea from a different perspective:
the average rate-of-change of a function \(f\)
on an interval of length \(h\) after some initial point \(x=c\) is
\[ \frac{f(c+h)-f(c)}{h}\,. \]
This expression is called the difference quotient of \(f\) at \(c.\)
On the graph of \(f\) this is the slope of the secant line that passes through
the points \(\bigl(c, f(c)\bigr)\) and \(\bigl(c+h, f(c+h)\bigr).\)
Same idea from a different perspective:
the average rate-of-change of a function \(f\)
on an interval of length \(h\) after some initial point \(x=c\) is
\[ \frac{f(c+h)-f(c)}{h}\,. \]
This expression is called the difference quotient of \(f\) at \(c.\)
On the graph of \(f\) this is the slope of the secant line that passes through
the points \(\bigl(c, f(c)\bigr)\) and \(\bigl(c+h, f(c+h)\bigr).\)