 A rational function is a quotient of polynomial functions.
The formula for a rational function \(f\) can be expressed
as \(f(x) = \frac{P(x)}{Q(x)}\) where \(P\) and \(Q\) are polynomials.
The roots (or zeros) of a polynomial function
are the input values \(x\) that yield an output of zero,
which correspond to the \(x\)-intercepts of the function’s graph.
For a rational function \(f = P/Q,\)
the roots of the numerator \(P\) correspond to roots of the function itself,
whereas the roots of the denominator \(Q\) correspond to poles of the function,
values at which the function \(f\) is not defined and must be excluded from the domain.
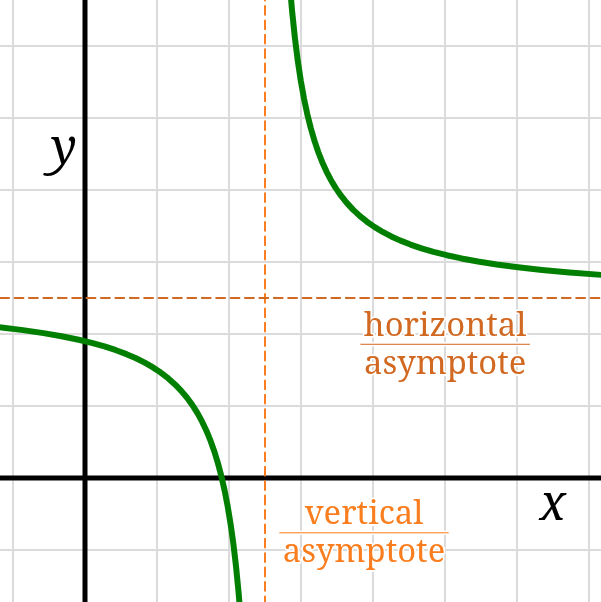
At each pole, the function’s graph will have a vertical asymptote,
a line that the graph “approaches” from either side.
In the language of limits, \(f\) has a vertical asymptote at \(x=c\)
if \(f\) is not defined at \(c\) and the limits
\(\lim_{x \to c^-} f(x)\) and \(\lim_{x \to c^+} f(x)\)
are each equal to either \(+\infty\) or \(-\infty.\)
A rational function is a quotient of polynomial functions.
The formula for a rational function \(f\) can be expressed
as \(f(x) = \frac{P(x)}{Q(x)}\) where \(P\) and \(Q\) are polynomials.
The roots (or zeros) of a polynomial function
are the input values \(x\) that yield an output of zero,
which correspond to the \(x\)-intercepts of the function’s graph.
For a rational function \(f = P/Q,\)
the roots of the numerator \(P\) correspond to roots of the function itself,
whereas the roots of the denominator \(Q\) correspond to poles of the function,
values at which the function \(f\) is not defined and must be excluded from the domain.
At each pole, the function’s graph will have a vertical asymptote,
a line that the graph “approaches” from either side.
In the language of limits, \(f\) has a vertical asymptote at \(x=c\)
if \(f\) is not defined at \(c\) and the limits
\(\lim_{x \to c^-} f(x)\) and \(\lim_{x \to c^+} f(x)\)
are each equal to either \(+\infty\) or \(-\infty.\)
 The degree of a polynomial function \(f\)
is the highest power of \(x\) that appears in the formula \(f(x).\)
The leading coefficient of a polynomial function \(f\)
is the coefficient of the term with that highest power.
If the degrees of \(P\) and \(Q\) of a rational function \(f = P/Q\) are equal
then the function’s graph will have a horizontal asymptote
at a height of \(y = m\) where \(m\) is the ratio
of the leading coefficients of \(P\) and \(Q.\)
In the language of limits, \(f\) has a horizontal asymptote at \(y=k\)
if \(\lim_{x \to \infty} f(x) = \lim_{x \to -\infty} f(x) = k.\)
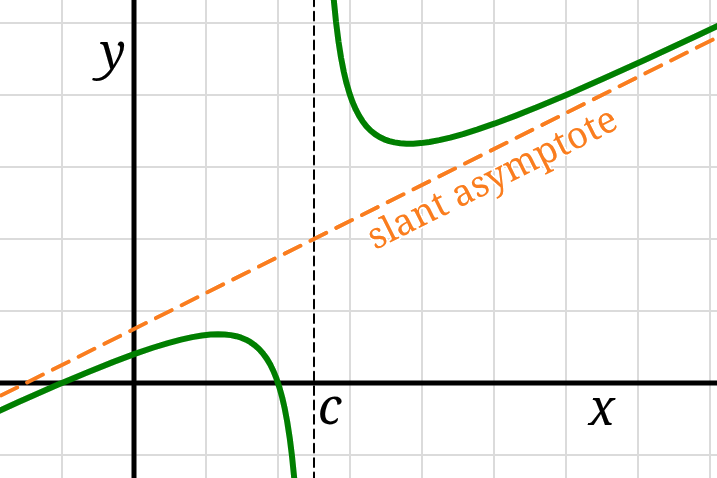
If the degree of \(P\) is one more than the degree of \(Q\) then the function’s graph
will have a slant asymptote (or oblique asymptote),
an asymptote that is the line \(y = ax\) with slope \(a,\)
where \(a\) is the leading coefficient of \(P.\)
The degree of a polynomial function \(f\)
is the highest power of \(x\) that appears in the formula \(f(x).\)
The leading coefficient of a polynomial function \(f\)
is the coefficient of the term with that highest power.
If the degrees of \(P\) and \(Q\) of a rational function \(f = P/Q\) are equal
then the function’s graph will have a horizontal asymptote
at a height of \(y = m\) where \(m\) is the ratio
of the leading coefficients of \(P\) and \(Q.\)
In the language of limits, \(f\) has a horizontal asymptote at \(y=k\)
if \(\lim_{x \to \infty} f(x) = \lim_{x \to -\infty} f(x) = k.\)
If the degree of \(P\) is one more than the degree of \(Q\) then the function’s graph
will have a slant asymptote (or oblique asymptote),
an asymptote that is the line \(y = ax\) with slope \(a,\)
where \(a\) is the leading coefficient of \(P.\)