A function of \(x\) is algebraic if it can be described by a formula defined purely in terms of algebraic operations on \(x\).
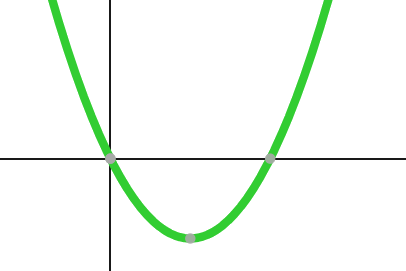
The graph of a function \(f\) will cross the \(y\)-axis at a single point at a height of \(f(0)\), a point called its \(y\)-intercept. A function’s graph may have several \(x\)-intercepts, points where it cross the \(x\)-axis. The \(x\) coordinates of these \(x\)-intercepts are called the roots or the zeros of \(f.\)
A linear function’s output changes at a constant rate (velocity) relative to its input; its graph is a line with constant slope (pitch, grade). A linear function with slope \(a\) and \(y\)-intercept \(b\) has formula \(f(x) = ax + b.\) A quadratic function’s output changes at a constantly changing rate (acceleration) relative to its input. Its graph is a parabolic curve. The vertex is the lowest or highest point on a parabola. A quadratic function with formula \({f(x) = ax^2+bx+c}\) has vertex located at the point \((h,k)\) and may have roots located at \(r_1\) and \(r_2\) for: \[ h = -\frac{b}{2a} \qquad\qquad k = \frac{b^2}{4a} + c \qquad\qquad r_1 = \frac{-b + \sqrt{b^2-4ac}}{2a} \qquad\qquad r_2 = \frac{-b - \sqrt{b^2-4ac}}{2a} \] In general, a polynomial function of degree (highest power) \(n\) will have at most \(n\) roots.