Inverse Trig (Cyclometric) Functions

  1. For each of the following right triangles, determine the measures of the unlabelled angles.
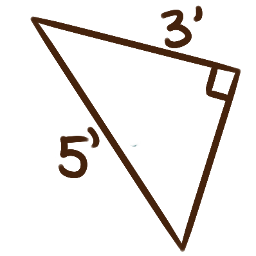
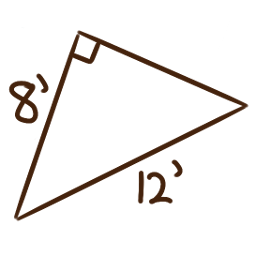
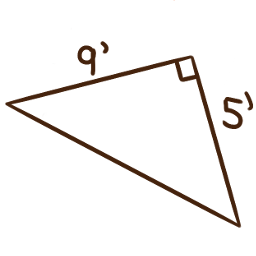
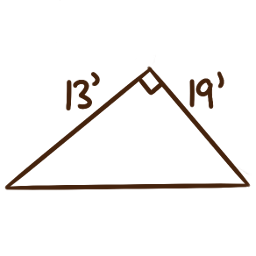
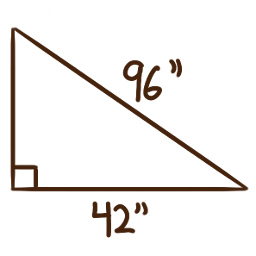
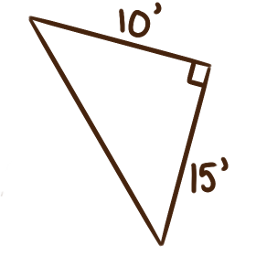
  2. Without referencing technology, by drawing the triangle suggested by the expression, determine the following output values.
    \(\displaystyle \cos\Bigl(\operatorname{arcsin}\bigl(3/5\bigr)\Bigr)\)
    \(\displaystyle \sin\Bigl(\operatorname{arccos}\bigl(33/65\bigr)\Bigr)\)
    \(\displaystyle \tan\Bigl(\operatorname{arccos}\bigl(99/101\bigr)\Bigr)\)
    \(\displaystyle \cos\Bigl(\operatorname{arctan}\bigl(24/7\bigr)\Bigr)\)
    \(\displaystyle \tan\Bigl(\operatorname{arccos}\bigl(21/221\bigr)\Bigr)\)
    \(\displaystyle \sin\Bigl(\operatorname{arctan}\bigl(11/60\bigr)\Bigr)\)
  3. Harriet the hiker is hiking an inclined hill. After reaching the top Harriet’s altimeter-pedometer multi-tool indicates that she gained 320′ in altitude and walked ½ a mile (2640′). What was the average angle (grade) of the incline of the hill?
  4. Billy the builder notices the accessibility ramp at the rear entrance of the courthouse starts 23′ from the entrance and rises to the entrance’s landing 2′ off the ground. Does this ramp meet the ADA requirement that accessibility ramps in public spaces have an incline of no more than 4.75°?
  5. Larry the lineman has just secured a 50′ guy-wire from the top of an electrical pole to the ground 37′ away from the pole’s base. His company requires that linemen install the wires at a guy angle between 30° and 45°, which means the wire should make an angle between 45° and 60° with the ground. Does Larry’s install meet his company’s requirement?