In three-dimensional space, we add a \(z\)-axis
perpendicular (orthogonal) to the usual \(x\)- and \(y\)-axis
to create a rectangular coordinate system called \(xyz\)-space.
The \(z\)-axis is oriented relative to the \(xy\)-plane
in accordance to the right-hand rule.
Any pair of axes span a coordinate plane,
and these coordinate planes split \(xyz\)-space into eight octants.
Each point can be described by a ordered triple \((x,y,z).\)
All computations from two-dimensional space
regarding either points or vectors
generalize to three-dimensional space in the most natural way.
Given two points \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2),\) the distance between them is \( \sqrt{(x_2\!-\!x_1)^2+(y_2\!-\!y_1)^2+(z_2\!-\!z_1)^2}, \) and their midpoint has coordinates \((\overline{x}, \overline{y}, \overline{z})\) given by the formulas \( \overline{x} = \frac{1}{2}(x_1\!+\!x_2) \) and \( \overline{y} = \frac{1}{2}(y_1\!+\!y_2) \) and \( \overline{z} = \frac{1}{2}(z_1\!+\!z_2).\) In three-dimensional space, two points uniquely determine a line and three non-colinear points uniquely determine a plane. A sphere of radius \(r\) centered at \((h,k,\ell)\) has equation \( r^2 = (x_2-h)^2+(y_2-k)^2+(z_2-\ell)^2\,. \) If a sphere intersects a plane in space, the resulting shape of their intersection, generically a circle, is called the trace of the sphere in the plane.
Vectors in \(xyz\)-space have three components.
The magnitude of \(\bm{v} = \langle v_1, v_2, v_3\rangle\) is calculated as
\(|\bm{v}| = \sqrt{v_1^2+v_2^2+v_3^2}\,.\)
In addition to the unit coordinate vectors
\({\mathbf{i} = \langle 1,0,0 \rangle}\)
and \({\mathbf{j} = \langle 0,1,0 \rangle,}\)
we now have \({\mathbf{k} = \langle 0,0,1 \rangle}\)
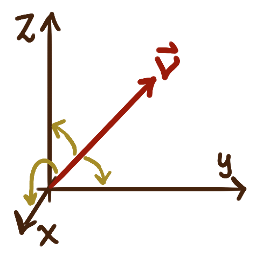For vectors \({\bm{u} = \langle u_1,u_2,u_3 \rangle}\)
and \({\bm{v} = \langle v_1,u_2,v_3 \rangle}\)
their dot product is calculated as
\({\bm{u}\cdot\bm{v} = u_1v_1 + u_2v_2 + u_3v_3} = |\bm{u}||\bm{v}|\cos(\theta).\)
The direction angles of a vector \(\bm{v}\)
are the three angles between \(\bm{v}\) and each of the three coordinate axes.
The cosines of these angles are referred to as the vector’s direction cosines.
If \(\alpha\) and \(\beta\) and \(\gamma\) are the direction angles of \(\bm{v}\)
with the \(x\)- and \(y\)- and \(z\)-axis respectively, then
\[
\cos(\alpha) = \frac{v_1}{|\bm{v}|}
\quad \cos(\beta) = \frac{v_2}{|\bm{v}|}
\quad \cos(\gamma) = \frac{v_2}{|\bm{v}|}
\qquad \bm{v} = \Bigl\langle |\bm{v}|\cos(\alpha), |\bm{v}|\cos(\beta), |\bm{v}|\cos(\gamma) \Bigr\rangle \,.
\]