 In addition to the coordinates of points on the unit circle,
and in addition to percentages,
the trigonometric functions can be thought of as returning
the ratios of side-lengths of a right triangle with acute angles.
\[
\sin\bigl(\theta\bigr) \!=\! \frac{\text{“opposite”}}{\text{“hypotenuse”}}
\qquad \cos\bigl(\theta\bigr) \!=\! \frac{\text{“adjacent”}}{\text{“hypotenuse”}}
\qquad \tan\bigl(\theta\bigr) \!=\! \frac{\text{“opposite”}}{\text{“adjacent”}}
% \csc\bigl(\theta\bigr) \!=\! \frac{\text{“hypotenuse”}}{\text{“opposite”}}
% \sec\bigl(\theta\bigr) \!=\! \frac{\text{“hypotenuse”}}{\text{“adjacent”}}
% \cot\bigl(\theta\bigr) \!=\! \frac{\text{“adjacent”}}{\text{“opposite”}}
\]
In addition to the coordinates of points on the unit circle,
and in addition to percentages,
the trigonometric functions can be thought of as returning
the ratios of side-lengths of a right triangle with acute angles.
\[
\sin\bigl(\theta\bigr) \!=\! \frac{\text{“opposite”}}{\text{“hypotenuse”}}
\qquad \cos\bigl(\theta\bigr) \!=\! \frac{\text{“adjacent”}}{\text{“hypotenuse”}}
\qquad \tan\bigl(\theta\bigr) \!=\! \frac{\text{“opposite”}}{\text{“adjacent”}}
% \csc\bigl(\theta\bigr) \!=\! \frac{\text{“hypotenuse”}}{\text{“opposite”}}
% \sec\bigl(\theta\bigr) \!=\! \frac{\text{“hypotenuse”}}{\text{“adjacent”}}
% \cot\bigl(\theta\bigr) \!=\! \frac{\text{“adjacent”}}{\text{“opposite”}}
\]
The other trigonometric functions
secant and cosecant and cotangent
can be defined in terms of sine and cosine.
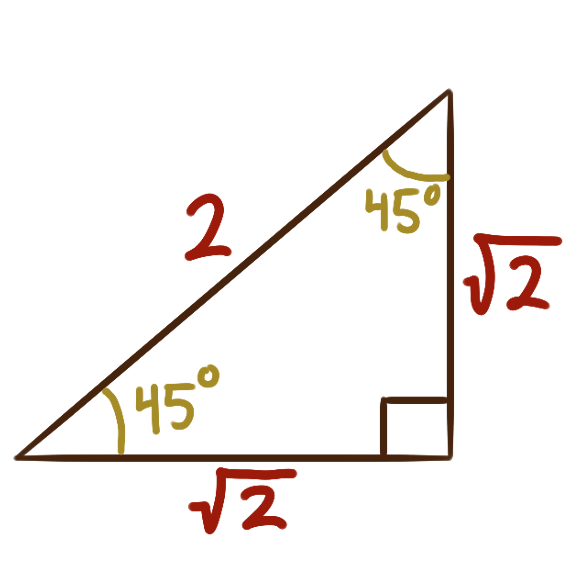
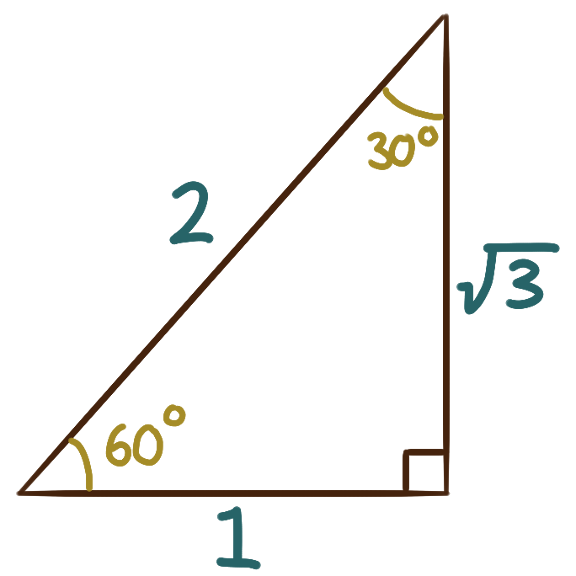 The three angles within any any triangle sum to 180°.
The right triangles with angles 30°-60°-90° and 45°-45°-90°
correspond to nice algebraic values of sine and cosine,
and so their side-lengths are in nice ratios to each other.
The supplement of an angle \(\theta\) is \(180°-\theta.\)
The complement of an angle \(\theta\) is \(90°-\theta.\)
The area of a triangle with an angle \(\theta\)
with initial and terminal side lengths \(a\) and \(b\)
is \(\frac{1}{2}ab\sin(\theta).\)
The three angles within any any triangle sum to 180°.
The right triangles with angles 30°-60°-90° and 45°-45°-90°
correspond to nice algebraic values of sine and cosine,
and so their side-lengths are in nice ratios to each other.
The supplement of an angle \(\theta\) is \(180°-\theta.\)
The complement of an angle \(\theta\) is \(90°-\theta.\)
The area of a triangle with an angle \(\theta\)
with initial and terminal side lengths \(a\) and \(b\)
is \(\frac{1}{2}ab\sin(\theta).\)