In the plane, after designating an origin point and two perpendicular cardinal axes — conventionally an \(x\)-axis whose positive direction points eastward and a \(y\)-axis whose positive direction points northward — we can describe the location of a point with its rectangular coordinates, an ordered pair \((a,b)\) where \(a\) is its position in the \(x\) direction and \(b\) is its position in the \(y\) direction. Altogether this imbues the plane with a rectangular (Cartesian) coordinate system, and we new refer to is as the \(xy\)-plane.
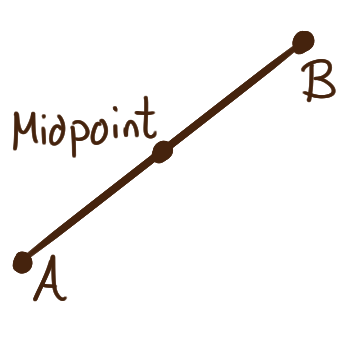 For two points \(A\) and \(B\) in the plane let \(\operatorname{d}(A,B)\)
denote the distance between them.
In terms of their coordinates \(\bigl(x_1,y_1\bigr)\) and \(\bigl(x_2,y_2\bigr)\),
the distance between those points is calculated by the formula
\(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\,. \)
Their midpoint, the point half-way between them,
has coordinates \({(\overline{x}, \overline{y})}\)
given by the formulas
\( {\overline{x} = \frac{1}{2} (x_1+x_2)} \)
and \( {\overline{y} = \frac{1}{2} (y_1+y_2)\,.} \)
For two points \(A\) and \(B\) in the plane let \(\operatorname{d}(A,B)\)
denote the distance between them.
In terms of their coordinates \(\bigl(x_1,y_1\bigr)\) and \(\bigl(x_2,y_2\bigr)\),
the distance between those points is calculated by the formula
\(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\,. \)
Their midpoint, the point half-way between them,
has coordinates \({(\overline{x}, \overline{y})}\)
given by the formulas
\( {\overline{x} = \frac{1}{2} (x_1+x_2)} \)
and \( {\overline{y} = \frac{1}{2} (y_1+y_2)\,.} \)
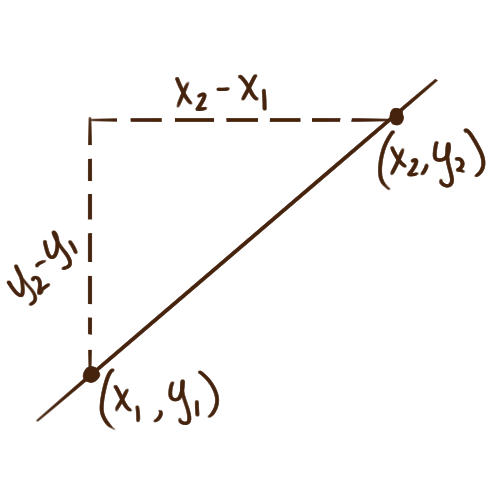 There is a unique line that passes through
any two points \(\bigl(x_1, y_1\bigr)\) and \(\bigl(x_2,y_2\bigr).\)
The slope of that line is
\( \displaystyle {m = (y_2-y_1)\,/\,(x_2-x_1);} \)
this is the “rate” at which the line is increasing/decreasing.
It’s also referred to as the pitch or grade of the line.
The “point-slope” form, and “slope-intercept” form,
and “general” form of a line are respectively given by the equations
\[ (y-y_1) = m(x-x_1) \qquad\qquad y = mx+b \qquad\qquad Ax + By = C \,. \]
Two lines are parallel if they never intersect,
in which case they must have the same slope.
Two lines are perpendicular (or normal, or orthogonal)
if they intersect at a right angle,
so one’s slope will be the negative reciprocal of the other.
There is a unique line that passes through
any two points \(\bigl(x_1, y_1\bigr)\) and \(\bigl(x_2,y_2\bigr).\)
The slope of that line is
\( \displaystyle {m = (y_2-y_1)\,/\,(x_2-x_1);} \)
this is the “rate” at which the line is increasing/decreasing.
It’s also referred to as the pitch or grade of the line.
The “point-slope” form, and “slope-intercept” form,
and “general” form of a line are respectively given by the equations
\[ (y-y_1) = m(x-x_1) \qquad\qquad y = mx+b \qquad\qquad Ax + By = C \,. \]
Two lines are parallel if they never intersect,
in which case they must have the same slope.
Two lines are perpendicular (or normal, or orthogonal)
if they intersect at a right angle,
so one’s slope will be the negative reciprocal of the other.
A circle is the curve consisting of all points that are a fixed distance, its radius, from a given point, its center. An equation corresponding to a circle with radius \(r\) and center with coordinates \((h,k)\) is \( (x-h)^2 +(y-k)^2 = r^2\,. \)
A circle of radius \(r\) has area \(\pi r^2\) and circumference \(2\pi r,\) where \(\pi \approx 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201988.\)