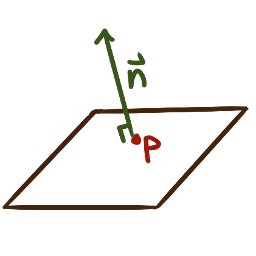
 A plane in space passing through a point \(P = (x_0, y_0, z_0)\)
with normal vector \(\bm{n} = \langle A, B, C \rangle\)
corresponds to the equation \({A(x-x_0) + B(y-y_0) + C(z-z_0) = 0.}\)
As a vector equation, for a generic vector \(\langle x,y,z \rangle\)
the equation of a plane is \({\bm{n} \cdot \bigl(\langle x,y,z \rangle-P\bigr) = 0}\)
There is a unique plane containing
any three non-colinear points in space.
Specifically, for points \(P\) and \(Q\) and \(R,\)
the normal vector of the plane will be
\(\bm{n} = \overrightarrow{PQ}\times\overrightarrow{PR}\)
and so its equation will be
\(\bm{n} \cdot \bigl(\langle x,y,z \rangle-P\bigr) = 0.\)
A plane in space passing through a point \(P = (x_0, y_0, z_0)\)
with normal vector \(\bm{n} = \langle A, B, C \rangle\)
corresponds to the equation \({A(x-x_0) + B(y-y_0) + C(z-z_0) = 0.}\)
As a vector equation, for a generic vector \(\langle x,y,z \rangle\)
the equation of a plane is \({\bm{n} \cdot \bigl(\langle x,y,z \rangle-P\bigr) = 0}\)
There is a unique plane containing
any three non-colinear points in space.
Specifically, for points \(P\) and \(Q\) and \(R,\)
the normal vector of the plane will be
\(\bm{n} = \overrightarrow{PQ}\times\overrightarrow{PR}\)
and so its equation will be
\(\bm{n} \cdot \bigl(\langle x,y,z \rangle-P\bigr) = 0.\)
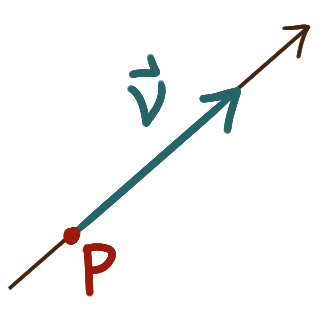 A line in three dimensional space must be described
either as the intersection of two planes
or as a vector equation of a parameter \(t.\)
The line passing through a point \(P = (x_0,y_0,z_0)\)
in the direction of the vector \(\bm{v} = \langle v_1,v_2,v_3 \rangle\)
can be described by the parametric equation
\[P+\bm{v}t = \bigl\langle x_0 + v_1t, y_0 + v_2t, z_0 + v_3t \bigr\rangle.\]
Two non-parallel planes in space will intersect along a line.
If the planes have normal vectors \(\bm{n}_1\) and \(\bm{n}_2,\)
then the direction vector of the line will be \(\bm{n}_1 \times \bm{n}_2,\)
and any solution to the system of equations consisting of the planes
will result in a point on the line.
A line in three dimensional space must be described
either as the intersection of two planes
or as a vector equation of a parameter \(t.\)
The line passing through a point \(P = (x_0,y_0,z_0)\)
in the direction of the vector \(\bm{v} = \langle v_1,v_2,v_3 \rangle\)
can be described by the parametric equation
\[P+\bm{v}t = \bigl\langle x_0 + v_1t, y_0 + v_2t, z_0 + v_3t \bigr\rangle.\]
Two non-parallel planes in space will intersect along a line.
If the planes have normal vectors \(\bm{n}_1\) and \(\bm{n}_2,\)
then the direction vector of the line will be \(\bm{n}_1 \times \bm{n}_2,\)
and any solution to the system of equations consisting of the planes
will result in a point on the line.
A plane in space and a line not parallel to that plane must intersect it at a point. For the plane \({\bm{n} \cdot \bigl(\langle x,y,z \rangle-P\bigr) = 0}\) and line \({\bigl\langle x_0 + v_1t, y_0 + v_2t, z_0 + v_3t \bigr\rangle}\) letting \({x = x_0 + v_1t}\) and \({y = y_0 + v_2t}\) and \({z = z+0 + v_3t}\) in the equation of the plane and solving will result in the value of \(t\) at which the line hits the plane, which, when plugged back into the equation of the line itself will result in the coordinates of the intersection point.