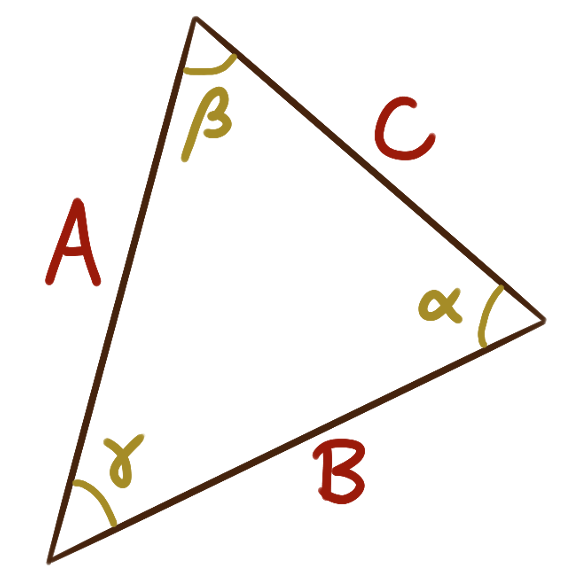 The law of sines and law of cosines are the names of two formulas
that extend what we know about solving right triangles —
calculating side-lengths and angle measures —
to any general triangle.
Among a triangle’s six features (three sides and three internal angles)
if we know the measures of three of those features
typically*
we can uniquely determine the entire triangle up to congruence.
For a triangle with internal angles measuring
\(\alpha\) and \(\beta\) and \(\gamma\)
that oppose sides of length \(A\) and \(B\) and \(C\) respectively,
we have the law of sines and the law of cosines:
\[
\frac{A}{\sin(\alpha)} = \frac{B}{\sin(\beta)} = \frac{C}{\sin(\gamma)}
\qquad \qquad
C^2 = A^2 + B^2 - 2AB\cos(\gamma)
\]
The law of sines and law of cosines are the names of two formulas
that extend what we know about solving right triangles —
calculating side-lengths and angle measures —
to any general triangle.
Among a triangle’s six features (three sides and three internal angles)
if we know the measures of three of those features
typically*
we can uniquely determine the entire triangle up to congruence.
For a triangle with internal angles measuring
\(\alpha\) and \(\beta\) and \(\gamma\)
that oppose sides of length \(A\) and \(B\) and \(C\) respectively,
we have the law of sines and the law of cosines:
\[
\frac{A}{\sin(\alpha)} = \frac{B}{\sin(\beta)} = \frac{C}{\sin(\gamma)}
\qquad \qquad
C^2 = A^2 + B^2 - 2AB\cos(\gamma)
\]
The law of cosines along with the \(\frac{1}{2}AB\sin(\gamma)\) formula for a triangle’s area, leads us to a formula for the area of a triangle strictly in terms of its side-lengths. Letting \(S = \frac{1}{2}(A+B+C),\) a number referred to as the semiperimeter of the triangle, the area of the triangle will be \(\sqrt{S(S-A)(S-B)(S-C)}.\) This is called Heron’s formula.
*Why can we only “typically” determine the triangle up to congruence? There is some nuance, a couple corner cases to consider:
- If we are given the measures of the three angles of a triangle, note first that this isn’t really three pieces of independent information; any one angle measure is determined by the other two. More to the point, per these angle measures, the triangle is only determined up to similarity: there is nothing that can be determined about the triangle’s side-lengths.
- Given the lengths of two sides and the measure of an angle that is opposite one of those sides, there may very well be two distinct triangles with these measurements.