 For two vectors
\(\bm{u} =\langle u_1,u_2,u_3 \rangle\) and \(\bm{v} = \langle v_1,v_2,v_3 \rangle,\)
their cross-product \(\bm{u}\times\bm{v}\)
is the vector computed as
\[
\begin{align*}
\bm{u}\times\bm{v}
= \operatorname{det}\!\begin{pmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}
\\ u_1 & u_2 & u_3
\\ v_1 & v_2 & v_3
\end{pmatrix}
&= \operatorname{det}\!\begin{pmatrix}u_2 & u_3 \\ v_2 & v_3\end{pmatrix}\mathbf{i}
- \operatorname{det}\!\begin{pmatrix}u_1 & u_3 \\ v_1 & v_3\end{pmatrix}\mathbf{j}
+ \operatorname{det}\!\begin{pmatrix}u_1 & u_2 \\ v_1 & v_2\end{pmatrix}\mathbf{k}
\\&= \Bigl\langle\big(u_2v_3\!-\!u_3v_2\big),
-\big(u_1v_3\!-\!u_3v_1\big),
\big(u_1v_2\!-\!u_2v_1\big)\Bigr\rangle\,.
\end{align*}
\]
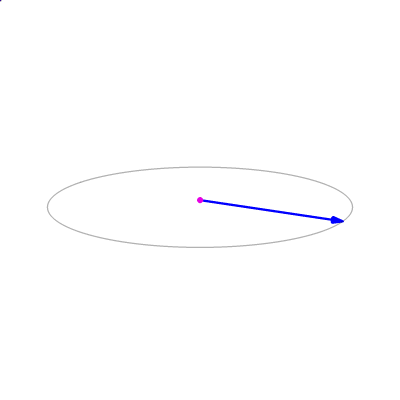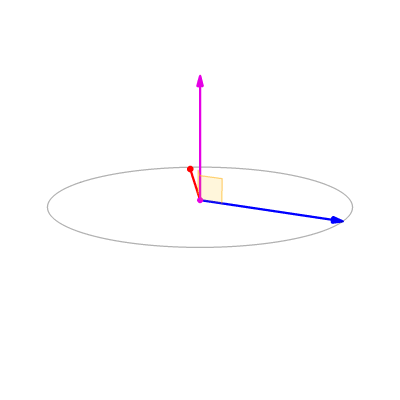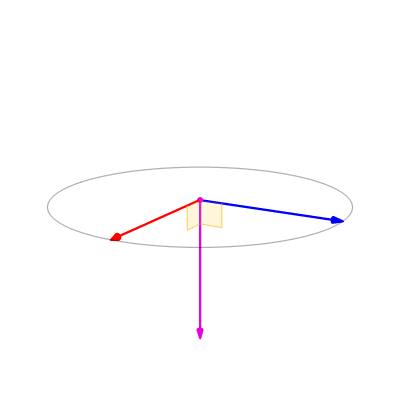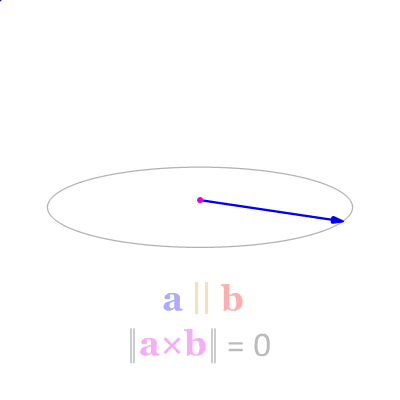
Generically the resulting vector will be orthogonal to both \(\bm{u}\) and \(\bm{v}\)
and will point in the direction indicated by the right-hand rule.
Its length will be proportional to the sine of the angle between \(\bm{u}\) and \(\bm{v}.\)
Specifically, the magnitude of the cross product will be
the product of the vectors’ individual magnitudes
weighted by the sine of the angle between them:
\(|\bm{u} \times \bm{v}| = |\bm{u}||\bm{v}|\sin(\theta).\)
Not coincidentally, this number also equals the area of the parallelogram
(twice the area of the triangle) framed by \(\bm{u}\) and \(\bm{v}\).
As a special case, two vectors \(\bm{u}\) and \(\bm{v}\) are parallel
if and only if \(\bm{u} \times \bm{v} = \bm{0}.\)
For two vectors
\(\bm{u} =\langle u_1,u_2,u_3 \rangle\) and \(\bm{v} = \langle v_1,v_2,v_3 \rangle,\)
their cross-product \(\bm{u}\times\bm{v}\)
is the vector computed as
\[
\begin{align*}
\bm{u}\times\bm{v}
= \operatorname{det}\!\begin{pmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}
\\ u_1 & u_2 & u_3
\\ v_1 & v_2 & v_3
\end{pmatrix}
&= \operatorname{det}\!\begin{pmatrix}u_2 & u_3 \\ v_2 & v_3\end{pmatrix}\mathbf{i}
- \operatorname{det}\!\begin{pmatrix}u_1 & u_3 \\ v_1 & v_3\end{pmatrix}\mathbf{j}
+ \operatorname{det}\!\begin{pmatrix}u_1 & u_2 \\ v_1 & v_2\end{pmatrix}\mathbf{k}
\\&= \Bigl\langle\big(u_2v_3\!-\!u_3v_2\big),
-\big(u_1v_3\!-\!u_3v_1\big),
\big(u_1v_2\!-\!u_2v_1\big)\Bigr\rangle\,.
\end{align*}
\]
Generically the resulting vector will be orthogonal to both \(\bm{u}\) and \(\bm{v}\)
and will point in the direction indicated by the right-hand rule.
Its length will be proportional to the sine of the angle between \(\bm{u}\) and \(\bm{v}.\)
Specifically, the magnitude of the cross product will be
the product of the vectors’ individual magnitudes
weighted by the sine of the angle between them:
\(|\bm{u} \times \bm{v}| = |\bm{u}||\bm{v}|\sin(\theta).\)
Not coincidentally, this number also equals the area of the parallelogram
(twice the area of the triangle) framed by \(\bm{u}\) and \(\bm{v}\).
As a special case, two vectors \(\bm{u}\) and \(\bm{v}\) are parallel
if and only if \(\bm{u} \times \bm{v} = \bm{0}.\)
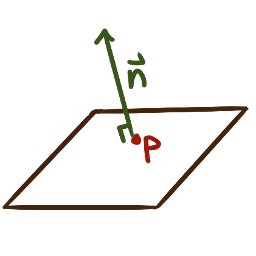 Given a plane in three-dimensional space
a vector \(\bm{n}\) is normal to the plane
if it is orthogonal to every vector parallel to the plane;
i.e. \(\bm{n}\cdot\bm{v}=0\)
for every vector \(\bm{v}\) parallel to the plane.
Three non-colinear points in space uniquely determine a plane.
Given three such points \(P\) and \(Q\) and \(R\)
we can calculate a vector normal to that plane as
\(\overrightarrow{PQ}\times\overrightarrow{PR}.\)
Given a plane in three-dimensional space
a vector \(\bm{n}\) is normal to the plane
if it is orthogonal to every vector parallel to the plane;
i.e. \(\bm{n}\cdot\bm{v}=0\)
for every vector \(\bm{v}\) parallel to the plane.
Three non-colinear points in space uniquely determine a plane.
Given three such points \(P\) and \(Q\) and \(R\)
we can calculate a vector normal to that plane as
\(\overrightarrow{PQ}\times\overrightarrow{PR}.\)
The scalar triple product of vectors \(\bm{u}\) and \(\bm{v}\) and \(\bm{w}\) is calculated as \(\bm{u} \cdot \bigl(\bm{v} \times \bm{w}\bigr)\) and gives the volume of the parallelepiped, the three-dimensional analog of a parallelogram, (and six times the volume of the tetrahedron) framed by those three vectors. Specifically, the vectors \(\bm{u}\) and \(\bm{v}\) and \(\bm{w}\) all lie in the same plane (are coplanar) if and only if \(\bm{u}\cdot\bigl(\bm{v}\times\bm{w}\bigr)=0.\)