Three-Dimensional Rectangular Geometry

Exercises

  1. Plot the points \((1,4,-6)\) and \((-2,3,6)\) and \((3,-4,-5)\) in \(xyz\)-space and determine which one is closest to the origin.
  2. What’s the distance between the points \((-6,7,-8)\) and \((0,21,-28)?\) What are the coordinates of the midpoint between those points?
  3. Consider a line segment with one endpoint at the coordinates \((4,1,2)\) and midpoint at the coordinates \((-3,4,5).\) What are the coordinates of the other endpoint?
  4. Sketch some \(xyz\)-coordinate axes, and sketch the planes \(x=4\) and \(y=5\) and \(z=-3\) and \(x=y\) in \(xyz\)-space.
  5. What’s an equation of the sphere with center \((4,5,-6)\) and radius three?
  6. The sphere \( (x-2)^2 +(y-3)^2 +(z+1)^2 =10\) intersects the \(xy\)-plane along a circle. What is the radius of this circle?

Problems & Challenges

  1. Consider the points \((1,1,1)\) and \((3,-3,8).\) Determine a point on the \(z\)-axis that is equidistant to those points.
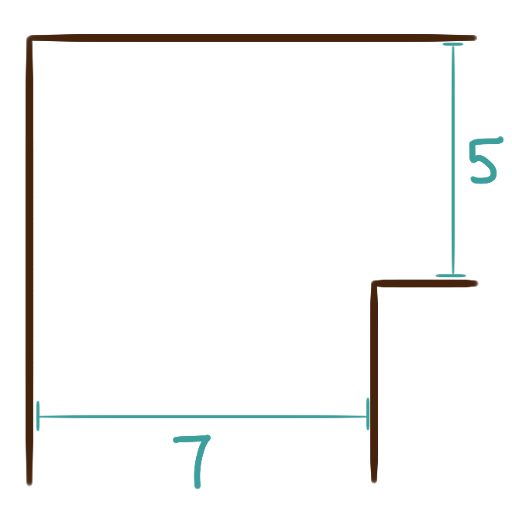
  2. Mr Goat is tethered to a stake in the ground at the concave corner of an “L”-shaped shed that is six feet tall. an image of how Mr Goat is tethered to the shed. Idk how to describe it accurately, so I'll work on making this an SVG file instead some day. The Genie of Goats happens to wander by and offer Mr Goat a wish, at which Mr Goat immediately wishes for the ability to fly. At a snap of his goat-fingers, the Genie of Goats grants his wish and disappears. Mr Goat can now fly! However he’s still tethered o the stake. Considering the length of Mr Goat’s tether and the dimensions of the shed indicated in the image, What is the volume of the region in which Mr Goat can fly around? Challenge: Suppose instead of that inner corner, Mr Goat were tethered to the upper-right corner indicated with a small square. Now what is the volume of the region in which Mr Goat can fly around?
  3. A right-angled halway corner as described in the prompt Suppose you have to transport a bunch of long, heavy, cast iron pipes one-by-one down a 7′ wide 8′ tall hallway, around a right-angled corner, and into a 5′ wide 8′ tall tall hallway. The pipes are awkward to carry around the corner but you can tilt them and carry them at an angle to make the task easier. You realize that getting longer pipes around the corner is going to be tough, and will be downright impossible if the pipe is too long. What’s the longest length of a pipe that you could possibly swivel around that corner?