Exercises
-
For each of the following right triangles, determine the lengths of the unlabelled sides and measures of the unlabelled angles.








-
For each of the following triples of numbers,
determine if there exists a triangle
with those numbers as the lengths of its sides,
and if so, determine if that triangle will be
acute, right, or obtuse.
\(\bigl\{6,7,8\bigr\}\)\(\bigl\{6,8,10\bigr\}\)\(\bigl\{6,8,11\bigr\}\)\(\bigl\{2,3,4\bigr\}\)\(\bigl\{2,3,6\bigr\}\)\(\bigl\{1,2,3\bigr\}\)\(\bigl\{5,12,12\bigr\}\)\(\bigl\{5,12,14\bigr\}\)\(\bigl\{5,12,17\bigr\}\)
-
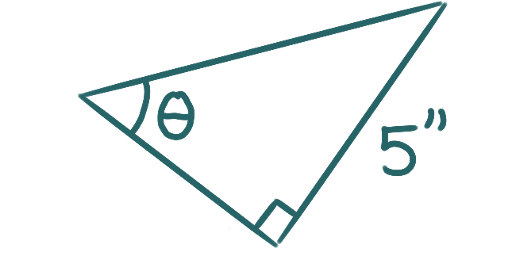
 Suppose that in each of the following triangles
that \(\cos(\theta) = \frac{3}{8}.\)
What must the lengths of the unlabelled sides of the triangle be?
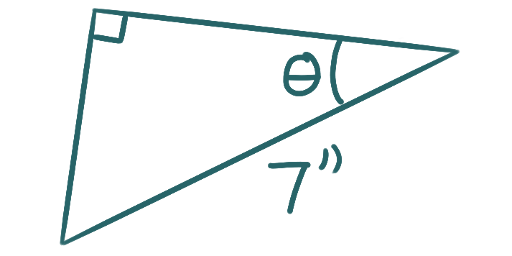
Suppose that in each of the following triangles
that \(\cos(\theta) = \frac{3}{8}.\)
What must the lengths of the unlabelled sides of the triangle be?
- A tree growing straight out of the ground casts a shadow on the level ground that is 15′ long. If the angle of inclination of the sun above the horizon is 51°, how tall is the tree?
- Harriet the hiker is hiking a hill that has an incline (grade) of 17°. If Harriet has climbed a distance of 2300′ along the incline, how much altitude (in feet) has she gained?
- Larry the lineman has just secured a 50′ guy-wire from the top of an electrical pole to the level ground away from the pole’s base. If the wire makes a 56° angle with the ground, how far from the pole is the wire anchored?
- Angeline is standing on level ground, some distance away from the base of St Mary’s Medical Center, which, at 150′ tall, is the tallest building in Grand Junction. Looking up at the very top of the building, Angeline pulls out her trusty inclinometer and measures that the angle of elevation of her line of sight is 72°. How far away is Angeline from the base of St Mary’s?
- Dr Baxter, bored with his daily commute home from work, decides to build a zip line from the roof of St Mary’s Medical Center to the nearby park that is in the direction of his house. St Mary’s is about 150′ tall. He decides he can afford to set up a zip line with a braking system, in which case experts recommend a 6% grade as the steepest direction of decline that is still safe. Sketching out the design, Dr Baxter has to figure out two things: assuming the zip line will be fairly taught, what angle will it make with the level ground in the park? And how long does the line itself need to be?
- Celina has climbed a tree! The tree is 33′ tall, growing straight out of level ground. She spots her friend away from the base of the tree and, pulling out her trusty inclinometer, measure the angle of depression towards her friend to be 53°. If her fiend pulls out an inclinometer too and measures the angle of inclination towards Celina, what should the measurement be? How far away from the base of the tree is Celina’s friend?
-
The Ladder Association
advises that, for safety’s sake, when setting up a ladder to be climbed,
the base of ladder should make at least a 75° angle with the ground.
Demetrius needs to buy a ladder to install rain gutters on his home.
He’s about 6′ tall, and the roofline of his house is 14′ off the ground.
- If Demetrius is dedicated to always setting up his ladder safely, what’s the shortest possible ladder he should buy?
- While out shopping for ladders, Demetrius notices there are painters working on ladders outside the hardware store. He notices that one painter’s ladder is 11′ long and positioned with its feet 3′ from the base of the wall. Should Demetrius go talk to the painter about safety?
- Looking at ladders in the ladder aisle of the hardware store, Demetrius notices that there are warnings on each ladder to not stand on top, or stand on the top rung. On every ladder for sale, the highest rung that’s safe to stand on is 2′ from the top of the ladder. What’s the shortest possible ladder that Demetrius, still dedicated to safety, should buy?
- Edith is flying a kite. She’s let out 123′ of kite string and, using her trusty inclinometer, measures that the kite’s angle of elevation from her position is 36°. Assuming the kite string is taught, what’s the kite’s altitude?
- Finneas is hiking to the top of a tall hill that has a constant incline of 25°. After reaching the top of the hill, his altimeter tells him his altitude changed by 6000′ since starting his hike. How long was the hike?
Problems & Challenges
- Suppose a right triangle has a pair of side-lengths measuring 7″ and 9″. What are the two possibilities for the measure of the third side?
- Suppose a right triangle of area \(5\) contains an acute angle \(\theta\) such that \(\tan(\theta) = 2.\) What are the side-lengths of the triangle?
-
Mr Goat is tethered to a stake in the ground
at the concave corner of an “L”-shaped shed.
The ground outside the shed is covered with lush delicious ground-cover —
grasses and clovers and creeping red thyme —
that Mr Goat would like to eat.
 Considering the length of Mr Goat’s tether
and the dimensions of the shed indicated in the image,
what is the total area of ground cover
that Mr Goat can raze?
Challenge:
Suppose instead of that inner corner,
Mr Goat were tethered to the upper-right corner
indicated with a small square.
Now what is the total area of ground cover
that Mr Goat can raze?
Considering the length of Mr Goat’s tether
and the dimensions of the shed indicated in the image,
what is the total area of ground cover
that Mr Goat can raze?
Challenge:
Suppose instead of that inner corner,
Mr Goat were tethered to the upper-right corner
indicated with a small square.
Now what is the total area of ground cover
that Mr Goat can raze?
-
 Consider three circles having radii measuring one, two, and three,
that are each mutually tangent to each other.
What is the area of the sector of the smallest circle
that is cut off by the two segments joining its center
to the centers of the others?
Consider three circles having radii measuring one, two, and three,
that are each mutually tangent to each other.
What is the area of the sector of the smallest circle
that is cut off by the two segments joining its center
to the centers of the others?