The Law of Sines & Law of Cosines

Exercises

  1. For each of the following triangles, determine the lengths of the unlabelled sides, measures of the unlabelled angles, and the area.
  2. Are any of the triangles above not uniquely defined by the information given? I.e. when determining the missing information about these triangles were there any that had multiple right answers?
  3. Staring at ground level, Harriet the hiker climbed 2300' up a hill that had an incline (grade) of 17°. She descended the other, steeper side of the hill, reaching ground level after travelling only 1700'. What was the average grade of the path of her descent?
  4. Larry the lineman has just secured a 50' guy-wire from the top of an electrical pole to the ground away from the pole’s base. The wire makes a 62° angle with the ground. He needs to secure a second guy-wire on the other side of the pole that anchors to the ground 43' from the first guy-wire’s anchor. How long does the second guy-wire need to be?

Problems & Challenges

  1. What is the distance between the points in the plane with polar coordinates \((3,45°)?\) and \((5,60°)?\) In general, given two points with polar coordinates \(\bigl(r_1, \theta_1\bigr)\) and \(\bigl(r_2, \theta_2\bigr),\) what is a formula for the distance between them?
  2. exactly as the prompt describes Consider three circles having radii measuring four, five, and six, that are each mutually tangent to each other. What is the area of the small region bound by these three circles?
  3. An airplane is cruising over the surface of the earth, maintaining a constant altitude. There are two radar antennas on the earth tracking the plane. The moment the plane flies directly over the great circle (geodesic) between them, the two antennas report this information: one reports that the plane is 21 miles away with an angle of elevation of 16.6° and the other antenna reports the plane is 46 miles away with an angle of elevation of 7.5°. Assuming the Earth is flat in the relatively short distance between them, how far apart are the antennas, and what is the plane’s altitude? How do the answers to those questions change if you factor in the curvature of the earth? (Recall the Earth’s radius is about 3960 miles.)
  4. A small airplane is cruising directly westward at a low altitude northwest of Grand Junction. The plane’s altimeter is broken, so the pilot decides to do some manual calculations to determine the plane’s altitude. Looking out the cockpit windows, she spots the familiar roadways below to use as reference. Specifically she identifies 24 Rd and 23 Rd, which she knows are one mile apart. Using her trusty pocket inclinometer to measure the angle of depression below the plane’s horizontal flightpath, she determines that 24 Rd is located at 16.7° and 23 Rd is located at 11.81°. What’s the straight-line distance between the plane and 23 Rd? What’s the plane’s altitude?
  5. A park ranger wants to measure the width of a river along a particular segment. He finds a spot where the riverbanks are relatively straight, and sees a nice birch tree across the river. Pulling out his handy pocket-sized theodolite he determines that, from his location on the riverbank, his line of sight towards the birch makes a 81° angle with the riverbank. Walking 45′ along the river, past the spot directly across the river from the tree, to a large lingonberry shrub, he stops to measure again, determining that his line of sight towards the birch makes a 72° angle with the riverbank. What’s the distance between the lingonberry shrub and the birch tree? How wide is the river?
  6. A lineworker named Lionel needs to stabilize an old power pole. He plans to attach to guy-wires in line with the pole, securing the tip of the pole to the ground. Lionel decides to use some pre-cut wires that have been sitting in the back of his truck for weeks. One wire is 57′ and the other is 63′. After securing the guy-wires, Lionel measures that the angle the 63′ wire makes with the ground is 38°. How are apart are spots where the wires are anchored in the ground?
  7. Elijah is hiking up mountain at a constant incline of 16°, directly towards the rising sun, which at the moment is elevated at an angle of 64° above the horizon — that is above the horizontal, not the incline of the mountain. Suddenly Elijah finds himself in the cool shade of something tall in front of him, but his relief is cut short when he notices that it’s a bear. A polar bear has stood up on its hind legs to scope out Elijah as a potential snack, the tip of its head just blocking the sun from Elijah’s eyes. Elijah knows that the average polar bear is about 12′ tall when standing on its hind legs, and that he’s 5′6″ tall. How far away is the polar bear standing from Elijah?
  8. The leaning tower of Pisa leans at about a 4° angle — it used to be much worse, but folks have been working on stabilizing the tower. Anyways, a US tourist is visiting the tower and does a very natural thing for a character in a math problem to do: starting at the base of the tower, he walks exactly 200′ away from the tower in the direction that it’s leaning, then, turning around and pulling out his inclinometer, notes that the angle of his gaze to the highest point he sees on the tower is 45°. How tall would the tower be if it were standing upright? (Assume the height of the tourist is negligible compared to the height of the tower.)
  9. Two cars on a salt flat in Utah are parked with their back bumpers touching. In an instant they each take off in straight trajectories that are 130° apart from each other, one car travelling at 100 mph and the other at 110mph. How far apart are the cars after one hour?
  10. Rafael the surveyor wants to install a slack line over a canyon. He scouts out some good spots on either side of the canyon to tether the line, but now needs to figure out how far apart they are. Using a his total station, from a fixed vantage point he measures that his distance to each spot is 345′ and 551′ and that the angle between those spots from his vantage points is 43°. How far apart are the two tether spots?
  11. A plane is flying at a constant speed of 550 mph. After flying for one hour the plane makes a course correction, changing its heading by 7° before flying for two hours in this new direction. How far is the plane from its starting location?
  12. A plane is flying over the ocean at a constant altitude along a straight path, when the pilot spots two ships on the ocean below lying on the intended track of the plane (i.e. the plane will fly directly over each of them). The radar aboard the plane indicates that one ship is 8 miles away at a angle of depression of 78°, and the other is 13 miles away at a angle of depression of 50°. How far apart are the two ships? What is the altitude of the plane?
  13. A crude drawing of the San Francisco Bay with two vectors pointing in different directions westward. Two ships sail from west from the San Francisco bay at the same time, one at a speed of 24 knots (nautical miles per hour) with a heading of N 67° W, and the other at a speed of 29 knots with a heading of S 41° W. Ignoring the curvature of the earth, how far are the ships from each other after six hours? How far apart are they considering the earth’s curvature?
  14. Portobello the pirate is sailing from island to island within a small archipelago searching for treasure. One morning, starting from his camp on the beach of the prettiest of the islands, A crude drawing to three islands arranged roughly as described and two direction vectors indicating the path of travel he sails 1.1 miles at a heading of N 14° E towards a small sandy island to search. Having found nothing on that island by midday he then sails 0.8 miles at a heading of N 77° E towards a small overgrown island to search. Having found nothing there either by dusk he decides to return to his camp. What direction and how far should he sail to get back?
  15. A small triangular plot of land bound by three roads has sides that measure 44′ and 65′ and 53′. What are the measures of the angles at the corners of plot of land? What is the area of that plot of land?
  16. The GPS coordinates of a location on the surface of the earth are based on the measure of the angle that location makes with the earth’s center. A location’s latitude is its angular distance north-south from the earth’s equator, and a location’s longitude is its angular distance east-west from the prime meridian, which is the meridian passing through the Royal Observatory in Greenwich, London. For example, the city of Grand Junction CO has a latitude of 39°05′16″N and a longitude of 108°34′05″W. Recall that the radius of the earth is approximately 3960 miles.
    1. How far along the surface of the earth would a person have to travel south from Grand Junction before they reached the equator?
    2. The city of Cincinnati, Ohio has approximately the same latitude as Grand Junction but a longitude of 84°30′45″W. How far apart along the surface of the earth are Grand Junction and Cincinnati?
    3. The city of Pyongyang, North Korea has approximately the same latitude as Grand Junction but a longitude of 125°44′51″E. How far apart along the surface of the earth are Grand Junction and Pyongyang?
  17. Given three numbers \(\alpha\) and \(\beta\) and \(\gamma\) that are measures of the internal angles of a triangle, that triangle is uniquely determined up to similarity (AAA). But not all triples of numbers are the internal angles of a triangle; how can you tell which triples of numbers can and can’t be the measures of a triangle’s angles?
  18. Up to congruence, there is a unique triangle with side-lengths \(7\) and \(8\) and \(9.\)
    1. Calculate the measure of the angles internal to this triangle, calculate the area of this triangle, and make an accurate drawing of this triangle.
    2. In general given three numbers \(A\) and \(B\) and \(C\) that are the side-lengths of a triangle, that triangle is uniquely determined up to congruence (SSS). But not all triples of numbers are the side-lengths of a triangle; how can you tell which triples of numbers can and can’t be the side-lengths of a triangle?

  19. Up to congruence, there is a unique triangle with side-lengths \(7\) and \(8\) and an angle between those sides that measures \(56°.\) Calculate the length of the remaining side and measures of the remaining angles internal to this triangle, calculate the area of this triangle, and make an accurate drawing of this triangle.

    Note that any triple of numbers \(A\) and \(\gamma\) and \(B\) uniquely define a triangle with side-lengths \(A\) and \(B\) with an angle of measure \(\gamma\) between them (SAS), allowing for “degenerate” triangles when \(\gamma\) is a multiple of 180°.

  20. Up to congruence, there is a unique triangle with side-length \(7\) and angles adjacent to that side measuring \(34°\) and \(56°.\)
    1. Calculate the lengths of the remaining sides and measure of the remaining angle internal to this triangle, calculate the area of this triangle, and make an accurate drawing of this triangle.
    2. In general given three numbers, a side-length of a triangle \(B\) and the measures of two angles adjacent to that side \(\alpha\) and \(\gamma,\) that triangle is uniquely determined up to congruence (ASA). But not all such triples of numbers determine a triangle uniquely; how can you tell which side-lengths \(B\) and angles \(\alpha\) and \(\gamma\) really do or don’t uniquely determine a triangle?
  21. Up to congruence, there are two distinct triangles with side-lengths \(7\) and \(8\) and an angle adjacent only to the latter side measuring \(56°.\)
    1. Determine these two possible triangles, and for each possibility calculate the length of the remaining side and measures of the remaining angles internal to the triangle, calculate the area of the triangle, and make an accurate drawing of the triangle.
    2. In general given three numbers, two side-lengths of a triangle \(A\) and \(B\) and the measure of an angle adjacent to the latter side \(\alpha,\) that triangle is sometimes uniquely determined up to congruence (SSA), but sometimes there is a second distinct triangle with those same measurements. Furthermore, not all such triples of numbers determine a triangle at all. How can you tell which side-lengths \(A\) and \(B\) and angles \(\alpha\) determine a unique triangle, which determine two distinct triangles, and which determine no triangle at all?
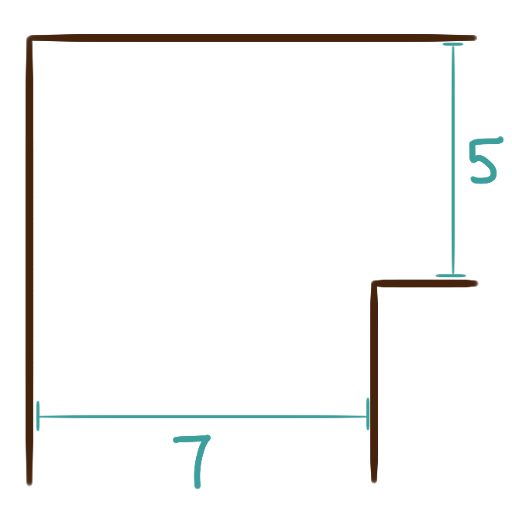  22. A right-angled halway corner as described in the prompt Suppose you have to transport a bunch of long, heavy, cast iron pipes one-by-one down a 7′ wide hallway, around a right-angled corner, and into a 5′ wide hallway. The pipes are awkward to carry so you decide to balance them on your shoulder, perfectly level with the ground, lest the pipe falls and damages the flooring. You realize that getting longer pipes around the corner is going to be tough, and will be downright impossible if the pipe is too long. What’s the longest length of a pipe that you could possibly swivel around that corner balanced on your shoulder?