-
For each of the following right triangles, calculate the measures of the unlabelled angles.
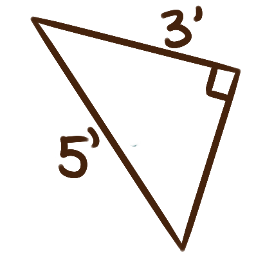
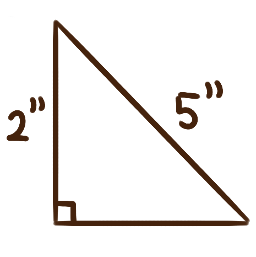
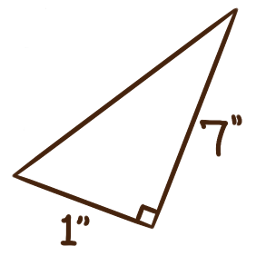
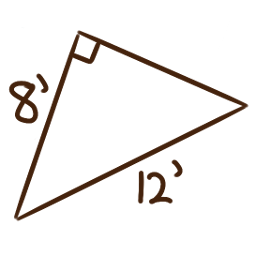
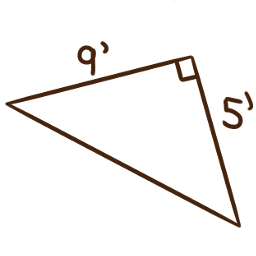
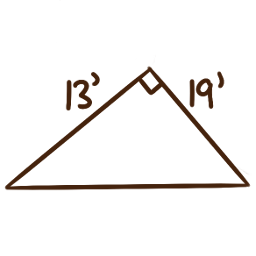
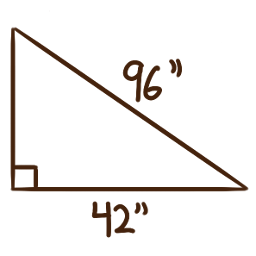
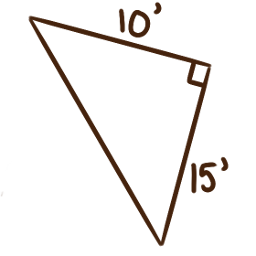
-
Without referencing technology,
by recognizing the input values
as familiar coordinates on the unit circle,
determine the following output values.
\(\displaystyle \operatorname{arcsin}\biggl(\frac{1}{2}\biggr)\)\(\displaystyle \operatorname{arcsin}\biggl(\frac{\sqrt{3}}{2}\biggr)\)\(\displaystyle \operatorname{arccos}\biggl(\frac{\sqrt{2}}{2}\biggr)\)\(\displaystyle \operatorname{arccos}\biggl(\frac{\sqrt{3}}{2}\biggr)\)\(\displaystyle \operatorname{arctan}\biggl(\frac{1}{\sqrt{3}}\biggr)\)\(\displaystyle \operatorname{arctan}\Bigl(\sqrt{3}\Bigr)\)\(\displaystyle \operatorname{arctan}\Bigl(-\sqrt{3}\Bigr)\)\(\displaystyle \operatorname{arcsin}\bigl(1\bigr)\)\(\displaystyle \operatorname{arccos}\bigl(0\bigr)\)\(\displaystyle \operatorname{arctan}\bigl(1\bigr)\)
-
Without referencing technology,
by drawing the triangle suggested by the expression,
determine the following output values.
\(\displaystyle \cos\Bigl(\operatorname{arcsin}\bigl(3/5\bigr)\Bigr)\)\(\displaystyle \sin\Bigl(\operatorname{arccos}\bigl(33/65\bigr)\Bigr)\)\(\displaystyle \tan\Bigl(\operatorname{arccos}\bigl(99/101\bigr)\Bigr)\)\(\displaystyle \cos\Bigl(\operatorname{arctan}\bigl(24/7\bigr)\Bigr)\)\(\displaystyle \tan\Bigl(\operatorname{arccos}\bigl(21/221\bigr)\Bigr)\)\(\displaystyle \sin\Bigl(\operatorname{arctan}\bigl(11/60\bigr)\Bigr)\)
- Write down four angles \(\theta\) between \(-360°\) and \(360°\) such that \(\tan\bigl(\theta\bigr) = 5.\)
- A 17′ tall tree growing straight out of the ground casts a shadow on the level ground that is 12′ long. What is the angle of inclination of the sun above the horizon?
- Harriet the hiker is hiking an inclined hill. After reaching the top Harriet’s altimeter-pedometer multi-tool indicates that she gained 320′ in altitude and walked ½ a mile (2640′). What was the average angle (grade) of the incline of the hill?
- Larry the lineman has just secured a 50′ guy-wire from the top of an electrical pole to the ground 37′ away from the pole’s base. His company requires that linemen install the wires at a guy angle between 30° and 45°, which means the wire should make an angle between 45° and 60° with the ground. Does Larry’s install meet his company’s requirement?
- Garamond is standing sad and alone in an empty parking lot. He is 5′10″ tall, and his shadow is 11′ long from his feet to the tip of his shadow-head. What is the angle of inclination of the sun?
- Henrietta wants to set up a camera to automatically record an aerial fireworks show. She positions the camera on the level ground about 500′ from where the fireworks will be launched, and Henrietta knows that, on average, these fireworks will launch 200′ in the air. At what angle of inclination should she tilt the camera to ensure she gets a good recording of the show?