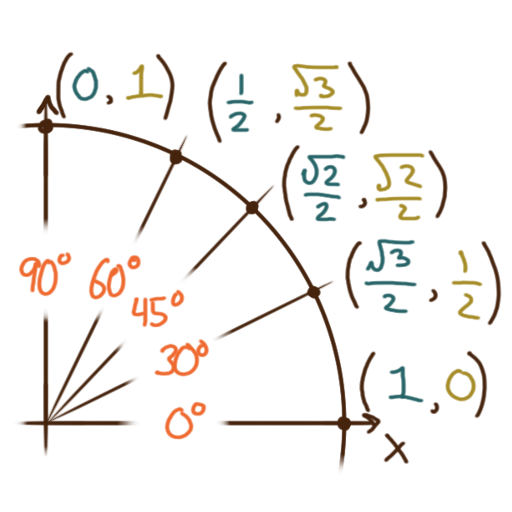 The unit circle is the circle of radius one centered at the origin.
On the unit circle, an angle of measure \(\theta\)
corresponds to the point \(\bigl(1\cos(\theta), 1\sin(\theta)\bigr);\)
i.e. in this context \(\cos(\theta)\) and \(\sin(\theta)\) are literal coordinates.
This is helpful for manually calculating some common input-output pairs for sine and cosine.
After knowing the input-output pairs in the first quadrant,
to calculate the sine and cosine of a common angle elsewhere
you must “reflect” these coordinates over the \(x\)- or \(y\)-axis,
making them negative as necessary.
There are four other trigonometric functions to know,
tangent and secant
and cotangent and cosecant,
as well as three Pythagorean identities
relating all these trigonometric functions.
Tangent is the only special function among them:
its output represents the slope of the line
passing through the origin inclined/declined at an angle of \(\theta.\)
The others you may take to just be a notational convenience.
The unit circle is the circle of radius one centered at the origin.
On the unit circle, an angle of measure \(\theta\)
corresponds to the point \(\bigl(1\cos(\theta), 1\sin(\theta)\bigr);\)
i.e. in this context \(\cos(\theta)\) and \(\sin(\theta)\) are literal coordinates.
This is helpful for manually calculating some common input-output pairs for sine and cosine.
After knowing the input-output pairs in the first quadrant,
to calculate the sine and cosine of a common angle elsewhere
you must “reflect” these coordinates over the \(x\)- or \(y\)-axis,
making them negative as necessary.
There are four other trigonometric functions to know,
tangent and secant
and cotangent and cosecant,
as well as three Pythagorean identities
relating all these trigonometric functions.
Tangent is the only special function among them:
its output represents the slope of the line
passing through the origin inclined/declined at an angle of \(\theta.\)
The others you may take to just be a notational convenience.
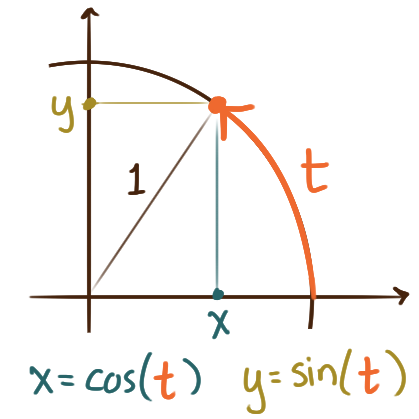 This all has a different interpretation
in terms of radian measure on the unit circle.
Imagine a point starting at \((1,0)\) and moving
around the perimeter of the unit circle counterclockwise,
tracing out an arc landing at a terminal point
corresponding to arc of length \(t.\)
Note that since this is the unit circle,
\(t\) is the radian measure of the angle
subtended by that traced arc.
Then in this radian measure, the terminal point
corresponding to \(t\) has coordinates \(\bigl(\cos(t), \sin(t)\bigr)\).
Just like every angle measured in degrees corresponds to
a principal angle between \(0°\) and \(360°,\)
any arclength \(t\) has a reference number \(\overline{t}\)
between \(0\) and \(2\pi\) that correspond to the same terminal point.
This all has a different interpretation
in terms of radian measure on the unit circle.
Imagine a point starting at \((1,0)\) and moving
around the perimeter of the unit circle counterclockwise,
tracing out an arc landing at a terminal point
corresponding to arc of length \(t.\)
Note that since this is the unit circle,
\(t\) is the radian measure of the angle
subtended by that traced arc.
Then in this radian measure, the terminal point
corresponding to \(t\) has coordinates \(\bigl(\cos(t), \sin(t)\bigr)\).
Just like every angle measured in degrees corresponds to
a principal angle between \(0°\) and \(360°,\)
any arclength \(t\) has a reference number \(\overline{t}\)
between \(0\) and \(2\pi\) that correspond to the same terminal point.