 A vector \(\bm{v}\) in two-dimensional space
is a pair \(\bm{v} = \langle v_1,v_2 \rangle\) that,
without any other context, denotes movement
from the origin to the point \(\bigl(v_1, v_2\bigr).\)
The numbers \(v_1\) and \(v_2\) are called
the horizontal and vertical components of the vector.
Sometimes we talk about the vector
from a point \(A\) to a point \(B,\)
which we’ll denote \(\overrightarrow{AB}.\)
The points \(A\) and \(B\) are referred to
as the initial and terminal point respectively.
Note that a symbol that represent a vector
will always be typeset in bold like \(\bm{v}\)
or handwritten with a small arrow decoration like \(\vec{v}.\)
This is to contrast with symbols that represent numbers,
now sometimes referred to as scalars,
which are typeset normally.
A vector \(\bm{v}\) in two-dimensional space
is a pair \(\bm{v} = \langle v_1,v_2 \rangle\) that,
without any other context, denotes movement
from the origin to the point \(\bigl(v_1, v_2\bigr).\)
The numbers \(v_1\) and \(v_2\) are called
the horizontal and vertical components of the vector.
Sometimes we talk about the vector
from a point \(A\) to a point \(B,\)
which we’ll denote \(\overrightarrow{AB}.\)
The points \(A\) and \(B\) are referred to
as the initial and terminal point respectively.
Note that a symbol that represent a vector
will always be typeset in bold like \(\bm{v}\)
or handwritten with a small arrow decoration like \(\vec{v}.\)
This is to contrast with symbols that represent numbers,
now sometimes referred to as scalars,
which are typeset normally.
 Whereas a scalar has only magnitude,
a vector has direction and magnitude,
and serves as a good model for a displacement, a velocity, or a force.
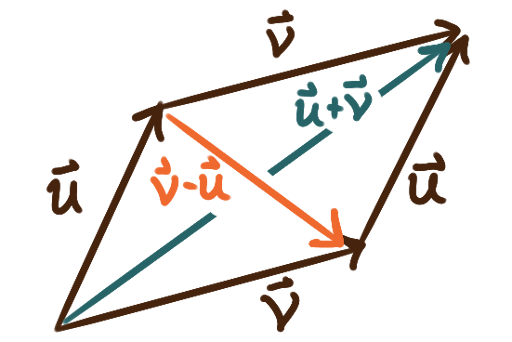
Given two vectors (forces) \(\bm{u}\) and \(\bm{v}\)
applied one after the other to a point (object),
the resultant vector (force) is the sum \(\bm{u}+\bm{v}.\)
If a vector (force) \(\bm{u}\) is scaled by a factor of \(k\)
then \(k\bm{u}\) will denote the scaled vector.
In terms of their components,
\[
\bm{u} = \langle u_1, u_2 \rangle
\quad
\bm{v} = \langle v_1, v_2 \rangle
\quad
\implies
\quad
\bm{u} + \bm{v} = \langle u_1+v_1, u_2+v_2 \rangle
\quad
k\bm{u} = \langle k u_1, k u_2 \rangle.
\]
The vector \(-\bm{v}\) will have the opposite direction as \(\bm{v}.\)
The length of a vector \(\bm{v}\)
is referred to as its magnitude (or sometimes its modulus),
and is denoted \(|\bm{v}|.\)
The magnitude of a vector \(\bm{v} = \langle v_1, v_2 \rangle\)
can be calculated explicitly in terms of its components as \(\sqrt{v_1^2 + v_2^2}.\)
There is a unique vector with no magnitude, indicating no movement,
called the zero vector, denoted \(\bm{0}.\)
A unit vector is a vector of length one;
given a vector \(\bm{v}\) the unit vector in the same direction as \(\bm{v}\)
will be denoted \(\bm{\hat{v}}\) (“vee hat”)
and calculated as \(\bm{\hat{v}} = \frac{1}{|\bm{v}|}\bm{v}.\)
The unit coordinate vectors \({\mathbf{i} = \langle 1,0 \rangle}\)
and \({\mathbf{j} = \langle 0,1 \rangle}\)
are the unit vectors pointing in the direction of each coordinate axis.
As a matter of notation, we sometimes write
\(\langle v_1,v_2 \rangle\) as \(v_1\mathbf{i} + v_2\mathbf{j}.\)
Whereas a scalar has only magnitude,
a vector has direction and magnitude,
and serves as a good model for a displacement, a velocity, or a force.
Given two vectors (forces) \(\bm{u}\) and \(\bm{v}\)
applied one after the other to a point (object),
the resultant vector (force) is the sum \(\bm{u}+\bm{v}.\)
If a vector (force) \(\bm{u}\) is scaled by a factor of \(k\)
then \(k\bm{u}\) will denote the scaled vector.
In terms of their components,
\[
\bm{u} = \langle u_1, u_2 \rangle
\quad
\bm{v} = \langle v_1, v_2 \rangle
\quad
\implies
\quad
\bm{u} + \bm{v} = \langle u_1+v_1, u_2+v_2 \rangle
\quad
k\bm{u} = \langle k u_1, k u_2 \rangle.
\]
The vector \(-\bm{v}\) will have the opposite direction as \(\bm{v}.\)
The length of a vector \(\bm{v}\)
is referred to as its magnitude (or sometimes its modulus),
and is denoted \(|\bm{v}|.\)
The magnitude of a vector \(\bm{v} = \langle v_1, v_2 \rangle\)
can be calculated explicitly in terms of its components as \(\sqrt{v_1^2 + v_2^2}.\)
There is a unique vector with no magnitude, indicating no movement,
called the zero vector, denoted \(\bm{0}.\)
A unit vector is a vector of length one;
given a vector \(\bm{v}\) the unit vector in the same direction as \(\bm{v}\)
will be denoted \(\bm{\hat{v}}\) (“vee hat”)
and calculated as \(\bm{\hat{v}} = \frac{1}{|\bm{v}|}\bm{v}.\)
The unit coordinate vectors \({\mathbf{i} = \langle 1,0 \rangle}\)
and \({\mathbf{j} = \langle 0,1 \rangle}\)
are the unit vectors pointing in the direction of each coordinate axis.
As a matter of notation, we sometimes write
\(\langle v_1,v_2 \rangle\) as \(v_1\mathbf{i} + v_2\mathbf{j}.\)