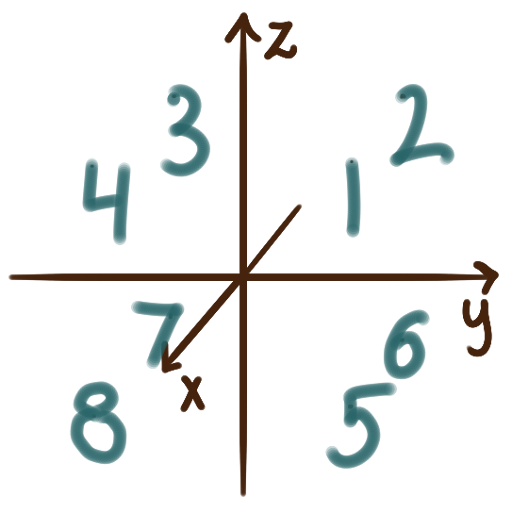In three-dimensional space, we add a \(z\)-axis
perpendicular (orthogonal) to the usual \(x\)- and \(y\)-axis
to create a rectangular coordinate system called \(xyz\)-space.
The \(z\)-axis is oriented relative to the \(xy\)-plane
in accordance to the right-hand rule.
Any pair of axes span a coordinate plane,
and these coordinate planes split \(xyz\)-space into eight octants.
Each point can be described by a ordered triple \((x,y,z).\)
All computations from two-dimensional space
regarding either points or vectors
generalize to three-dimensional space in the most natural way.
Given two points \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2),\)
the distance between them is \( \sqrt{(x_2\!-\!x_1)^2+(y_2\!-\!y_1)^2+(z_2\!-\!z_1)^2}, \)
and their midpoint has coordinates \((\overline{x}, \overline{y}, \overline{z})\)
given by the formulas
\( \overline{x} = \frac{1}{2}(x_1\!+\!x_2) \)
and \( \overline{y} = \frac{1}{2}(y_1\!+\!y_2) \)
and \( \overline{z} = \frac{1}{2}(z_1\!+\!z_2).\)
In three-dimensional space, two points uniquely determine a line and three non-colinear points uniquely determine a plane. More generally, a locally one-dimensional space is called a curve and a locally two-dimensional space is called a surface. Any single equation involving \(x\) and \(y\) and \(z\) analytically defines a surfaces in three-dimensional space, whereas curves, specifically lines, can’t be described by a single equation; curves must be defined as the intersection of two surfaces, and so they need two equations, the equations of those surfaces, to be described analytically.
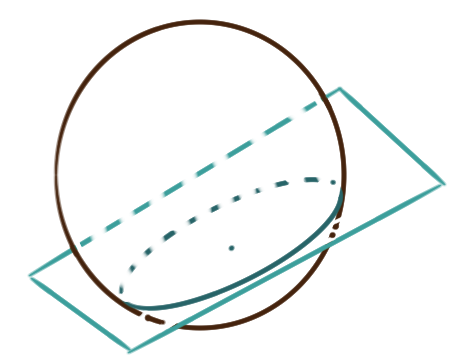A sphere of radius \(r\) centered at \((h,k,\ell)\)
has equation \( r^2 = (x-h)^2+(y-k)^2+(z-\ell)^2\,. \)
If a sphere intersects a plane in space,
the resulting shape of their intersection, generically a circle,
is called the trace of the sphere in that plane.