“Right Triangle” Trigonometry

TK In addition to the coordinates of points on the unit circle, and in addition to percentages (scaling factors), the trigonometric functions can be thought of as returning the ratios of side-lengths of a right triangle with acute angles. \[ \sin\bigl(\theta\bigr) \!=\! \frac{\text{“opposite”}}{\text{“hypotenuse”}} \qquad \cos\bigl(\theta\bigr) \!=\! \frac{\text{“adjacent”}}{\text{“hypotenuse”}} \qquad \tan\bigl(\theta\bigr) \!=\! \frac{\text{“opposite”}}{\text{“adjacent”}} % \csc\bigl(\theta\bigr) \!=\! \frac{\text{“hypotenuse”}}{\text{“opposite”}} % \sec\bigl(\theta\bigr) \!=\! \frac{\text{“hypotenuse”}}{\text{“adjacent”}} % \cot\bigl(\theta\bigr) \!=\! \frac{\text{“adjacent”}}{\text{“opposite”}} \]

The other trigonometric functions secant and cosecant and cotangent can be defined in terms of sine and cosine.

\(\displaystyle \sec\bigl(\theta\bigr) \!=\! \frac{1}{\cos\bigl(\theta\bigr)}\)
\(\displaystyle \csc\bigl(\theta\bigr) \!=\! \frac{1}{\sin\bigl(\theta\bigr)}\)
\(\displaystyle \cot\bigl(\theta\bigr) \!=\! \frac{1}{\tan\bigl(\theta\bigr)}\)
\(\displaystyle \sin^2\bigl(\theta\bigr) \!+\! \cos^2\bigl(\theta\bigr) \!=\! 1\)
\(\displaystyle \tan^2\bigl(\theta\bigr) \!+\! 1 \!=\! \sec^2\bigl(\theta\bigr)\)
\(\displaystyle 1 \!+\! \cot^2\bigl(\theta\bigr) \!=\! \csc^2\bigl(\theta\bigr)\)

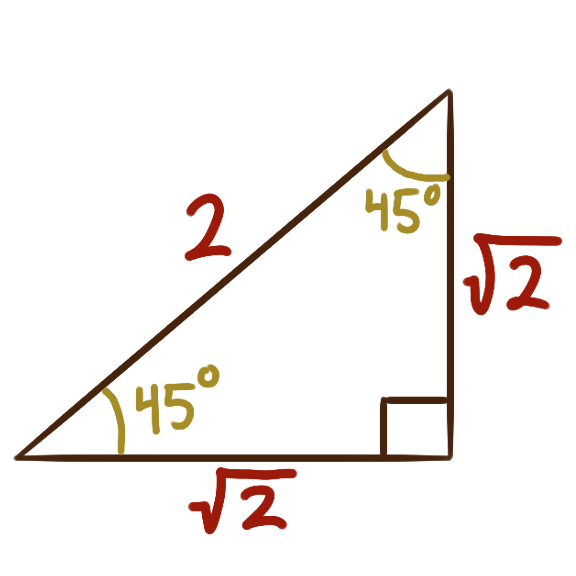
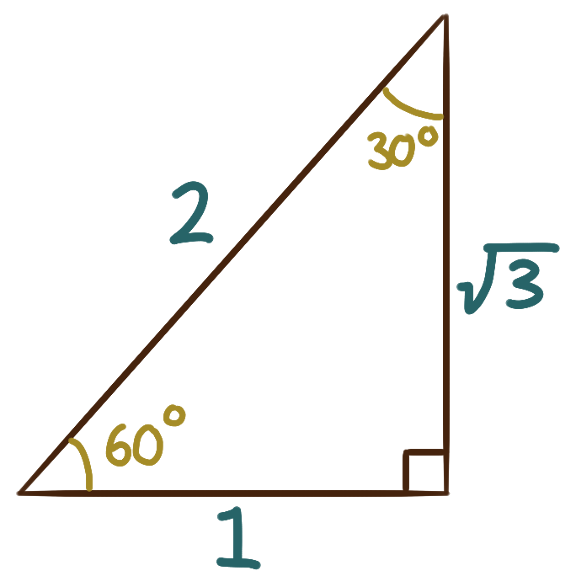a 45-45-90 triangle a 30-60-90 triangle The three angles within any any triangle sum to 180°. The right triangles with angles 30°-60°-90° and 45°-45°-90° correspond to nice algebraic values of sine and cosine. Two angles \(\theta\) and \(\varphi\) are complementary if \(\theta + \varphi = 90°;\) the two non-right angles in a right triangle are complements. Two angles \(\theta\) and \(\varphi\) are supplementary if \(\theta + \varphi = 180°,\) if they together they form a half-rotation, i.e. lie along a straight line.

The area of a triangle with sides of lengths \(A\) and \(B\) and an angle between them that measures \(\theta\) is \(\frac{1}{2}AB\sin\bigl(\theta\bigr).\)