In the plane,
after designating a pole (the origin)
and a single polar axis conventionally pointing eastward,
we can describe the location of a point with its polar coordinates,
an ordered pair \((r,\theta)\)
where \(r\) is the length of the segment from the origin to the point
and \(\theta\) is the measure of the angle from the polar axis to the segment.
Positive \(\theta\) corresponds to counterclockwise rotation.
Altogether this constitutes the polar coordinate system.
Trigonometric functions are necessary to convert between
the rectangular and polar coordinates of a point.
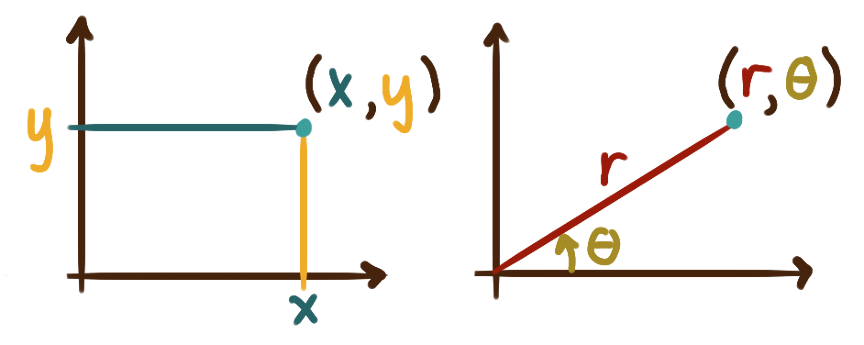 \[
\begin{align*}
x&=r\cos(\theta)
\\ y&=r\sin(\theta)
\end{align*}
\quad
\longleftrightarrow
\quad
\begin{align*}
r&=\sqrt{x^2+y^2}
\\ \theta&=\operatorname{arctan}\Bigl(\frac{y}{x}\Bigr) \;(\text{kinda})
\end{align*}
\]
The sine (sin) and cosine (cos) functions
should be thought as returning percentages by which the radius \(r\) is scaled
as it’s projected onto the polar and normal axes.
The arctangent function (tan-1)
should be thought of as taking a slope as input
and returning an angle of incline/decline between -90° and 90° as output;
if \(x\) is negative, you’ve got to think a bit about the output \(\theta.\)
The polar coordinates of a point are not unique.
E.g. the coordinates
\((r,\theta)\) and \((r,360°+\theta)\) and \((-r,180°+\theta)\)
all refer to the same point.
Note that a negative radius corresponds
to the direction away from the point.
However each point has a unique “principal” pair of polar coordinates,
where \({r \gt 0}\) and \({0 \leq \theta \lt 360°.}\)
\[
\begin{align*}
x&=r\cos(\theta)
\\ y&=r\sin(\theta)
\end{align*}
\quad
\longleftrightarrow
\quad
\begin{align*}
r&=\sqrt{x^2+y^2}
\\ \theta&=\operatorname{arctan}\Bigl(\frac{y}{x}\Bigr) \;(\text{kinda})
\end{align*}
\]
The sine (sin) and cosine (cos) functions
should be thought as returning percentages by which the radius \(r\) is scaled
as it’s projected onto the polar and normal axes.
The arctangent function (tan-1)
should be thought of as taking a slope as input
and returning an angle of incline/decline between -90° and 90° as output;
if \(x\) is negative, you’ve got to think a bit about the output \(\theta.\)
The polar coordinates of a point are not unique.
E.g. the coordinates
\((r,\theta)\) and \((r,360°+\theta)\) and \((-r,180°+\theta)\)
all refer to the same point.
Note that a negative radius corresponds
to the direction away from the point.
However each point has a unique “principal” pair of polar coordinates,
where \({r \gt 0}\) and \({0 \leq \theta \lt 360°.}\)
Note that \(\sin \theta\) and \(\sin(\theta)\) mean the same thing. Also it’s conventional to write \(\sin^2(\theta)\) for \(\bigl(\sin(\theta)\bigr)^2.\) However \(\tan^{-1}(\theta) \neq \bigl(\tan(\theta)\bigr)^{-1};\) a power of \(-1\) on a function denotes its inverse function whereas the latter denote the reciprocal of the output.
When \(r = 1,\) because they’re the \(x\)- and \(y\)-coordinate on a circle of radius one, \(\sin^2\bigl(\theta\bigr) + \cos^2\bigl(\theta\bigr) = 1.\) This is called a Pythagorean identity.