Given two vectors \(\bm{u} = \langle u_1,u_2 \rangle\) and \(\bm{v} = \langle v_1,v_2 \rangle,\) their dot product \(\bm{u}\cdot\bm{v}\) (sometimes called the scalar product or inner product) is the number defined as the result of the calculation \(\bm{u}\cdot\bm{v} = u_1 v_1 + u_2 v_2.\) Alternatively if \(\theta\) is the angle between \(\bm{u}\) and \(\bm{v},\) then \(\bm{u}\cdot\bm{v} = |\bm{u}||\bm{v}|\cos(\theta).\) These definitions are equivalent due to the law of cosines. If two vectors are perpendicular (orthogonal) then \(\bm{u}\cdot\bm{v} =0,\) and if two vectors are parallel then \(\bm{u}\cdot\bm{v} = |\bm{u}||\bm{v}|.\) Intuitively then, the dot product is the product of the magnitudes of two vectors “correcting for” how much they aren’t pointing in the same direction. The dot product is commutative: \(\bm{u}\cdot\bm{v}=\bm{v}\cdot\bm{u}.\)
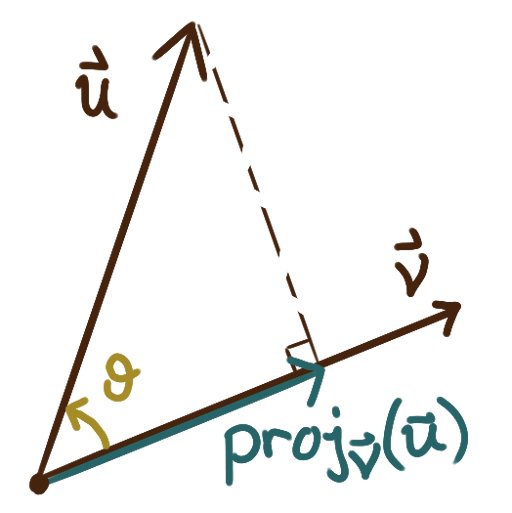The projection of \(\bm{u}\) onto \(\bm{v}\) (a vector),
denoted \(\operatorname{proj}_{\bm{v}}(\bm{u}),\)
is calculated as
\[
\operatorname{proj}_{\bm{v}}(\bm{u})
= \bigl(|\bm{u}|\cos(\theta)\bigr)\bm{\hat{v} }
= \Bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{v}|}\Bigr)\bm{\hat{v}}
= \Bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{v}|^2}\Bigr)\bm{v}
\]
Imagine a light shines directly down, perpendicularly, onto \(\bm{v};\)
\(\operatorname{proj}_{\bm{v}}(\bm{u})\) is the “shadow” that \(\bm{u}\) casts onto \(\bm{v}.\)
The component of \(\bm{u}\) along \(\bm{v}\) (a number)
is the length of the projection of \(\bm{u}\) onto \(\bm{v},\) i.e.
\[
\bigl|\operatorname{proj}_{\bm{v}}(\bm{u})\bigr|
= |\bm{u}|\cos(\theta)
= \frac{|\bm{u}\cdot\bm{v}|}{|\bm{v}|}
\]
For a vector \(\bm{v},\) let \(\bm{v}^\perp\) (“vee perp”) denote the vector perpendicular (orthogonal) to \(\bm{v}\) and of the same magnitude such that, following the right-hand rule, the counterclockwise angle from \(\bm{v}\) to \(\bm{v}^\perp\) is 90°. In terms of its components, if \(\bm{v} = \langle v_1,v_2\rangle\) then \(\bm{v}^\perp = \langle -v_2,v_1\rangle.\) We can resolve a vector \(\bm{u}\) with respect to a coordinate system defined by \(\bm{v}\) and \(\bm{v}^\perp\) by writing it as a sum of orthogonal vectors, \[ \bm{u} = \bigl(|\bm{u}|\cos(\theta)\bigr)\bm{\hat{v}} + \bigl(|\bm{u}|\sin(\theta)\bigr)\bm{\hat{v}}^\perp = \Bigl(\operatorname{proj}_{\bm{v}}(\bm{u})\Bigr) + \Bigl(\operatorname{proj}_{\bm{v}^\perp}(\bm{u})\Bigr) = \Bigl(\operatorname{proj}_{\bm{v}}(\bm{u})\Bigr) + \Bigl(\bm{u} - \operatorname{proj}_{\bm{v}}(\bm{u})\Bigr) \,. \]