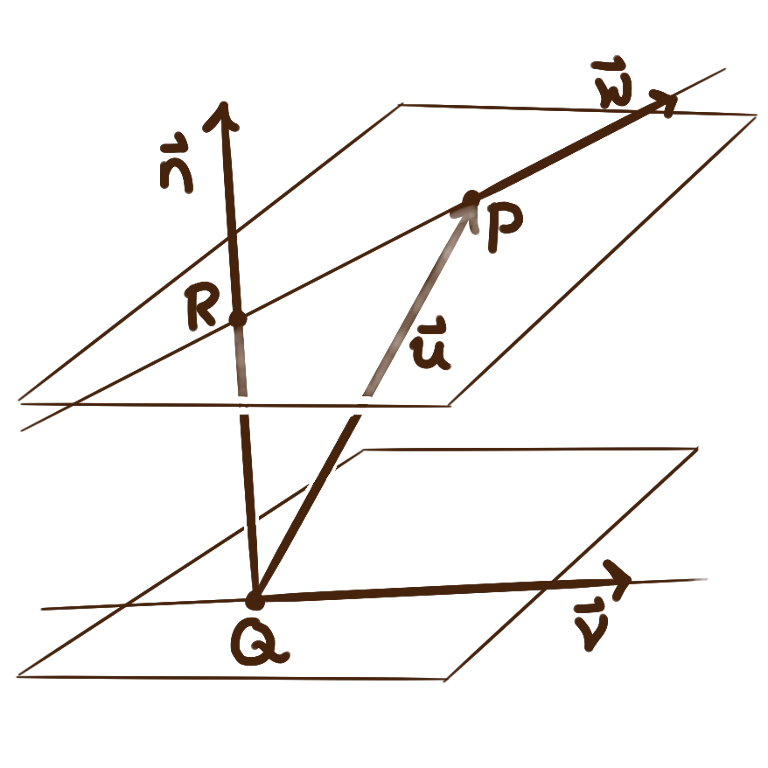
Compute the shortest distance to a plane from a point not on that plane.
Call the point \(P,\) and let \(R\) be the point on the plane closest to \(P.\) Let \(\bm{n}\) be a vector normal to the plane and let \(Q\) be the coordinates of any point on the plane, both of which can be inferred from an equation for the plane. Let \(\bm{u}\) be the vector from \(Q\) to \(P.\) The distance from \(P\) to the plane — the distance between \(P\) to \(R\) — will be the length of the vector \(\operatorname{proj}_{\bm{n}}(\bm{v}),\) which can be computed nicely as \( \bigl|\operatorname{proj}_{\bm{n}}(\bm{u})\bigr| = \bigl|\frac{\bm{u}\cdot\bm{n}}{|\bm{n}|}\bm{\hat n}\bigr| = \frac{|\bm{u}\cdot\bm{n}|}{|\bm{n}|} \,. \)
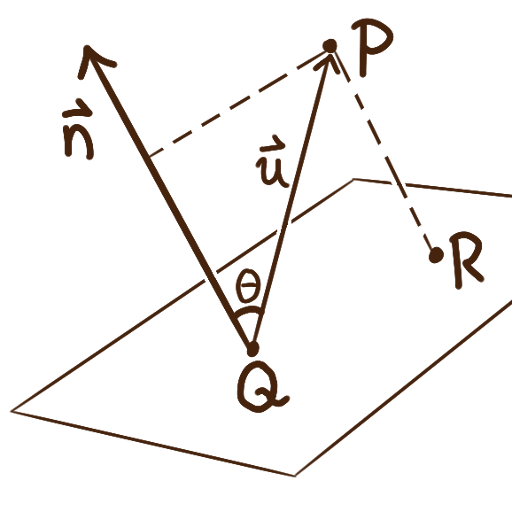
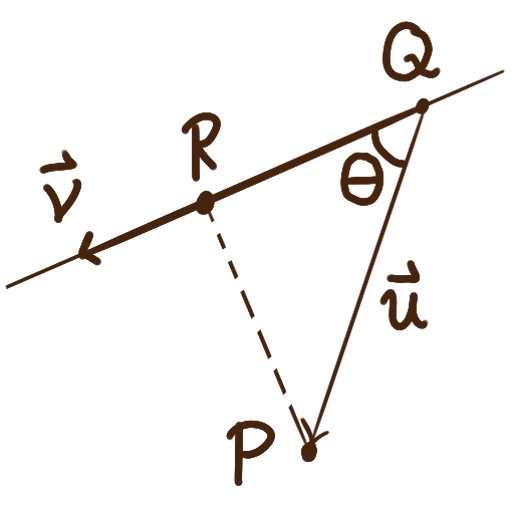
Compute the shortest distance to a line from a point not on that line.
Call the point \(P,\) and let \(R\) be the point on the line closest to \(P.\) Let \(\bm{v}\) be the direction vector of the line and let \(Q\) be the coordinates of any point on the line, both of which can be inferred from an parameterization of the line. Let \(\theta\) be the angle between \(\bm{u}\) and \(\bm{v}.\) which can be computed as \( \theta = \operatorname{arccos}\bigl(\frac{\bm{u}\cdot\bm{v}}{|\bm{u}||\bm{v}|}\bigr)\,. \) Considering the right triangle \(\triangle PQR,\) the distance from \(P\) to the plane — the distance between \(P\) to \(R\) — will be \(|\bm{u}\sin\bigl(\theta\bigr)|.\)
Compute the shortest distance between two skew (non-intersecting) lines.
Let \(P + \bm{w}t\) and \(Q + \bm{v}t\) be parameterizations of the two lines. If the lines are parallel, i.e. \(\bm{w}\) and \(\bm{v}\) are parallel, then the distance between the lines will be the distance from the point \(P\) to the line \(Q + \bm{v}t.\) Otherwise for each line, there is a unique plane containing that line that doesn’t intersect the other line. I.e. there is a pair of parallel planes containing those lines. Each plane will have normal vector \({\bm{n} = \bm{w}\times\bm{v},}\) and the distance between the lines will be the distance from \(Q\) to the plane containing \(P.\)